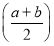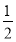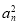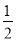题目内容
观察以下等式:
sin230°+cos260°+sin 30°·cos 60°=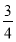 ,
,
sin240°+cos270°+sin 40°·cos 70°=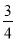 ,
,
sin215°+cos245°+sin 15°·cos 45°=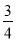 .
.
…
写出反映一般规律的等式,并给予证明.
sin2α+cos2(α+30°)+ sin α·cos(α+30°)=
【解析】反映一般规律的等式是(表述形式不唯一):
sin2α+cos2(α+30°)+ sin α·cos(α+30°)= .
.
证明如下:
sin2α+cos2(α+30°)+sin α·cos(α+30°)
=sin2α+(cos α·cos 30°-sin α·sin 30°)2
+sin α·(cos αcos 30°-sin α·sin 30°)
=sin2α+ 2+
2+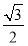 sin α ·cos α-
sin α ·cos α- sin2α
sin2α
=sin2α+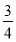 cos2α+
cos2α+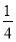 sin2α-
sin2α-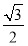 sin α·cos α+
sin α·cos α+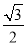 sin α·cos α-
sin α·cos α-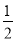 sin2α=
sin2α=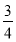 (sin2α+cos2α)=
(sin2α+cos2α)=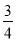 .
.

练习册系列答案
相关题目