题目内容

已知函数f（x）=sinx，对于满足0＜x1＜x2＜π的任意x1，x2，给出下列结论：
①（x2-x1）[f（x2）-f（x1）]＞0；②x2f（x1）＞x1f（x2）；③f（x2）-f（x1）＜x2-x1；④
f(x1)+f(x2)
2
＜f(
x1+x2
2
)，
其中正确结论的个数为______．
∵f（x）=sinx在[0，π]上的图象为

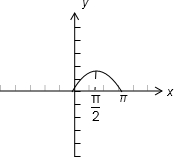
由图象知，f（x）在[0，
π
2
]上单调递增，在[
π
2
，π]单调递减，故①错
对于②，x2f（x1）＞x1f（x2）即为
f(x1)
x1
＞
f(x2)
x2
即表示两个点（x1，f（x1））；（x2，f（x2））与原点连线的斜率，由图知，两个斜率大小不确定，故②错
对于③f（x2）-f（x1）＜x2-x1即
f(x2)-f(x1)
x2-x1
＜0即表示两个点（x1，f（x1））；（x2，f（x2））连线的斜率，由图知，斜率的符号不确定．故③错
对于④，因为由图知，图象呈上凸趋势，所以有
f(x1)+f(x2)
2
＜f(
x1+x2
2
)，故④对
故答案为1
练习册系列答案
相关题目
已知函数f（x）的定义域为[-3，+∞），且f（6）=f（-3）=2．f′（x）为f（x）的导函数，f′（x）的图象如图所示．若正数a，b满足f（2a+b）＜2，则
b+3
a-2
的取值范围是（　　）
A．（-
3
2
，3）		B．（-∞，-
3
2
）∪（3，+∞）
C．（-
9
2
，3）		D．（-∞，-
9
2
）∪（3，+∞）
某公司试销一种成本单价为500元的新产品，规定试销时销售单价不低于成本单价，又不高于800元．经试销调查，发现销售量y（件）与销售单价x（元）之间的关系可近似看作一次函数y=kx+b（k≠0），函数图象如图所示．
（1）根据图象，求一次函数y=kx+b（k≠0）的表达式；
（2）设公司获得的毛利润（毛利润=销售总价-成本总价）为S元．试问销售单价定为多少时，该公司可获得最大毛利润？最大毛利润是多少？此时的销售量是多少？
已知函数f（x）=4x2-4ax+a2-2a+2在区间[0，2]上有最小值3，求实数a的值．
已知函数f（x）=3-|x|，g（x）=x2-4x+3，构造函数F（x），定义如下：当f（x）≥g（x）时，F（x）=g（x）；当f（x）＜g（x）时，F（x）=f（x），则F（x）在[-3，3]（　　）
A．有最大值3，最小值-1
B．有最大值7-2
7
，无最小值
C．有最大值3，无最小值
D．无最大值，也无最小值
设f(x)=
sin(
π
2
x+
π
4
)		(x≤2008)
f(x-5)(x＞2008)
，则f（2007）+f（2008）+f（2009）+f（2010）=______．
已知函数f（x）=
x+2，x≤-3
x2，-3＜x＜3
2x，x≥3
，若f（x）=3，则x=______．
设函数f（x）是R上的减函数，若f（m-1）＞f（2m+1），则实数m的取值范围是______．
已知函数f（x）=
x2
1+x2
，则f（1）+f（2）+f（3）+f（4）+f（5）+f（
1
2
）+f（
1
3
）+f（
1
4
）+f（
1
5
）=______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网