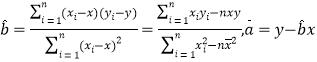题目内容
【题目】已知
为数列
的前
项和，
，
，若关于正整数的不等式
的解集中的整数解有两个，则正实数
的取值范围为（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】分析：由2Sn=（n+1）an，n≥2时，2Sn﹣1=nan﹣1，则2an=2（Sn﹣Sn﹣1），整理得：
，则
，可得：an=n．不等式an2﹣tan≤2t2，化为：（n﹣2t）（n+t）≤0，t＞0，0＜n≤2t，关于正整数n的不等式an2﹣tan≤2t2的解集中的整数解有两个，即可得出正实数t的取值范围．
详解：∵a1=1，2Sn=（n+1）an，
∴n≥2时，2Sn﹣1=nan﹣1，
∴2an=2（Sn﹣Sn﹣1）=（n+1）an﹣nan﹣1，整理得：，
∴
∴an=n．
不等式an2﹣tan≤2t2，化为：（n﹣2t）（n+t）≤0，t＞0，
∴0＜n≤2t，
关于正整数n的不等式an2﹣tan≤2t2的解集中的整数解有两个，
可知n=1，2．
∴1≤t＜
，
故答案为：A.
练习册系列答案
相关题目
【题目】中央电视台播出的《朗读者》节目，受到广大人民群众的喜爱.随着节目的播出，极大激发了观众对朗读以及经典的阅读学习积累的热情，从中获准匪浅，现从观看节目的观众中随机统计了4位观众的周均阅读学习经典的知识的时间（单位：小时）与年龄（单位：岁），并制作了对照表（如下表所示）：
年龄 | 20 | 30 | 40 | 50 |
周均学习成语知识时间 | 2.5 | 3 | 4 | 4.5 |
由表中数据，试求线性回归方程
，并预测年龄为50岁观众周均学习阅读经典知识的时间.
参考公式：
