Question

【题目】在平面直角坐标中，圆与圆相交与两点．

（I）求线段的长．

（II）记圆与轴正半轴交于点，点在圆C上滑动，求面积最大时的直线的方程．

Answer 1

【答案】（I）；（II）或．

【解析】

（I）先求得相交弦所在的直线方程，再求得圆的圆心到相交弦所在直线的距离，然后利用直线和圆相交所得弦长公式，计算出弦长.（II）先求得当时，取得最大值，根据两直线垂直时斜率的关系，求得直线的方程，联立直线的方程和圆的方程，求得点的坐标，由此求得直线的斜率，进而求得直线的方程.

（I）由圆O与圆C方程相减可知，相交弦PQ的方程为．

点（0，0）到直线PQ的距离，

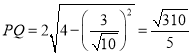
（Ⅱ），.

当时，取得最大值．

此时，又则直线NC为．

由，或

当点时，，此时MN的方程为．

当点时，，此时MN的方程为．

∴MN的方程为或．