题目内容
【题目】椭圆Γ: ![]() =1(a>b>0)的左右焦点分别为F1 , F2 , 焦距为2c,若直线y=
=1(a>b>0)的左右焦点分别为F1 , F2 , 焦距为2c,若直线y= ![]() 与椭圆Γ的一个交点M满足∠MF1F2=2∠MF2F1 , 则该椭圆的离心率等于 .
与椭圆Γ的一个交点M满足∠MF1F2=2∠MF2F1 , 则该椭圆的离心率等于 .
【答案】![]()
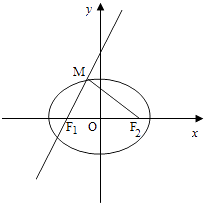
【解析】解:如图所示,
由直线y= ![]() 可知倾斜角α与斜率
可知倾斜角α与斜率 ![]() 有关系
有关系 ![]() =tanα,∴α=60°.
=tanα,∴α=60°.
又椭圆Γ的一个交点满足∠MF1F2=2∠MF2F1 , ∴ ![]() ,∴
,∴ ![]() .
.
设|MF2|=m,|MF1|=n,则 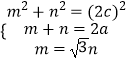 ,解得
,解得 ![]() .
.
∴该椭圆的离心率e= ![]() .
.
故答案为 ![]() .
.
由直线y= ![]() 可知斜率为
可知斜率为 ![]() ,可得直线的倾斜角α=60°.又直线与椭圆Γ的一个交点M满足∠MF1F2=2∠MF2F1 , 可得
,可得直线的倾斜角α=60°.又直线与椭圆Γ的一个交点M满足∠MF1F2=2∠MF2F1 , 可得 ![]() ,进而
,进而 ![]() .
.
设|MF2|=m,|MF1|=n,利用勾股定理、椭圆的定义及其边角关系可得 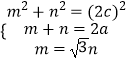 ,解出a,c即可.
,解出a,c即可.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
【题目】某大学餐饮中心为了了解新生的饮食习惯,在某学院大一年级![]() 名学生中进行了抽样调查,发现喜欢甜品的占
名学生中进行了抽样调查,发现喜欢甜品的占![]() .这
.这![]() 名学生中南方学生共
名学生中南方学生共![]() 人。南方学生中有
人。南方学生中有![]() 人不喜欢甜品.
人不喜欢甜品.
(1)完成下列![]() 列联表:
列联表:
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | |||
北方学生 | |||
合计 |
(2)根据表中数据,问是否有![]() 的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(3)已知在被调查的南方学生中有![]() 名数学系的学生,其中
名数学系的学生,其中![]() 名不喜欢甜品;有
名不喜欢甜品;有![]() 名物理系的学生,其中
名物理系的学生,其中![]() 名不喜欢甜品.现从这两个系的学生中,各随机抽取
名不喜欢甜品.现从这两个系的学生中,各随机抽取![]() 人,记抽出的
人,记抽出的![]() 人中不喜欢甜品的人数为
人中不喜欢甜品的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:![]() .
.
| 0.15 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |



