题目内容
【题目】以直角坐标系的原点O为极点，x轴正半轴为极轴，并在两种坐标系中取相同的长度单位，已知直线l的参数方程为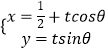 
，（t为参数，0＜θ＜π），曲线C的极坐标方程为ρsin2θ﹣2cosθ=0．
（1）求曲线C的直角坐标方程；
（2）设直线l与曲线C相交于A，B两点，当θ变化时，求|AB|的最小值．
【答案】
（1）解：由ρsin2θ﹣2cosθ=0，得ρ2sin2θ=2ρcosθ．
∴曲线C的直角坐标方程为y2=2x
（2）解：将直线l的参数方程代入y2=2x，得t2sin2θ﹣2tcosθ﹣1=0．
设A，B两点对应的参数分别为t1，t2，
则 
， 
， 
= 
= 
．
当 
时，|AB|的最小值为2
【解析】（1）利用极坐标与直角坐标的转化方法，求曲线C的直角坐标方程；（2）将直线l的参数方程代入y2=2x，得t2sin2θ﹣2tcosθ﹣1=0，利用参数的几何意义，求|AB|的最小值．
暑假作业海燕出版社系列答案【题目】学校为了了解高三学生每天自主学习中国古典文学的时间，随机抽取了高三男生和女生各50名进行问卷调查，其中每天自主学习中国古典文学的时间超过3小时的学生称为“古文迷”，否则为“非古文迷”，调查结果如表：
古文迷 | 非古文迷 | 合计 | |
男生 | 26 | 24 | 50 |
女生 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
（Ⅰ）根据表中数据能否判断有60%的把握认为“古文迷”与性别有关？
（Ⅱ）现从调查的女生中按分层抽样的方法抽出5人进行调查，求所抽取的5人中“古文迷”和“非古文迷”的人数；
（Ⅲ）现从（Ⅱ）中所抽取的5人中再随机抽取3人进行调查，记这3人中“古文迷”的人数为ξ，求随机变量ξ的分布列与数学期望．
参考公式：K2= 
，其中n=a+b+c+d．
参考数据：
P（K2≥k0） | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
k0 | 0.455 | 0.708 | 1.321 | 3.841 | 5.024 | 6.635 |
