题目内容
17.一个几何体的侧视图是边长为2的正三角形,正视图与俯视图的尺寸如图所示,则此几何体的体积为( )
| A. | 12+2$\sqrt{3}$+3π | B. | 12+3π | C. | $\sqrt{3}$π+2$\sqrt{3}$ | D. | $\frac{\sqrt{3}π}{3}$+2$\sqrt{3}$ |
分析 由三视图得到圆几何体,然后由圆锥和三棱锥体积公式得答案.
解答 解:由几何体的三视图可得原几何体如图,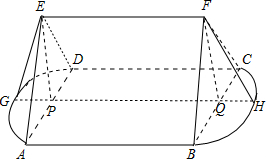
则几何体为两个半圆锥及中间一个平放的三棱柱的组合体,
∵左视图EAD为边长为2的正三角形,∴圆锥的高EP=$\sqrt{3}$,
∴两个半圆锥的体积和为$\frac{1}{3}π×{1}^{2}×\sqrt{3}=\frac{\sqrt{3}}{3}π$;
中间三棱柱的体积为$\frac{1}{2}×2×\sqrt{3}×2=2\sqrt{3}$.
∴几何体的体积为$\frac{\sqrt{3}}{3}π+2\sqrt{3}$.
故选:D.
点评 本题考查空间几何体的三视图,关键是由三视图得到原几何体,考查了学生的空间想象能力和思维能力,是中档题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
2.已知向量$\overrightarrow{a}$=(1,k),$\overrightarrow{b}$=(-4,2),$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$垂直,那么k的值为( )
| A. | -2 | B. | 1 | C. | -3或1 | D. | 2或3 |
9.一种集合A={3,5,x},B={2},若A∪B=A,则实数x的值为( )
| A. | -2 | B. | 2 | C. | 3 | D. | 5 |
 如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,OA⊥底面ABCD,OA=2,M为OA的中点.则异面直线OB与MD所成角余弦值为$\frac{\sqrt{10}}{10}$.
如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,OA⊥底面ABCD,OA=2,M为OA的中点.则异面直线OB与MD所成角余弦值为$\frac{\sqrt{10}}{10}$.