题目内容
设A(x1,y1).B(x2,y2)两点在抛物线y=2x2上,l是AB的垂直平分线.
1)当且仅当x1+x2取何值时,直线l经过抛物线的焦点F?证明你的结论;
2)当直线l的斜率为2时,求l在y轴上截距的取值范围.
1)当且仅当x1+x2取何值时,直线l经过抛物线的焦点F?证明你的结论;
2)当直线l的斜率为2时,求l在y轴上截距的取值范围.
(Ⅰ)∵抛物线y=2x2,即x2=
,∴p=
,
∴焦点为F(0,
)
(1)直线l的斜率不存在时,显然有x1+x2=0
(2)直线l的斜率存在时,设为k,截距为b
即直线l:y=kx+b由已知得:
⇒
⇒
⇒x12+x22=-
+b≥0⇒b≥
.
即l的斜率存在时,不可能经过焦点F(0,
)
所以当且仅当x1+x2=0时,直线l经过抛物线的焦点F
(II)设直线l的方程为:y=2x+b,
故有过AB的直线的方程为y=-
x+m,代入抛物线方程有2x2+
x-m=0,得x1+x2=-
.
由A、B是抛物线上不同的两点,于是上述方程的判别式△=
+8m>0,也就是:m>-
.
由直线AB的中点为(
,
)=(-
,
+m),
则
+m=-
+b,于是:b=
+m>
-
=
.
即得l在y轴上的截距的取值范围是(
,+∞).
| y |
| 2 |
| 1 |
| 4 |
∴焦点为F(0,
| 1 |
| 8 |
(1)直线l的斜率不存在时,显然有x1+x2=0
(2)直线l的斜率存在时,设为k,截距为b
即直线l:y=kx+b由已知得:
|
⇒
|
|
⇒x12+x22=-
| 1 |
| 4 |
| 1 |
| 4 |
即l的斜率存在时,不可能经过焦点F(0,
| 1 |
| 8 |
所以当且仅当x1+x2=0时,直线l经过抛物线的焦点F
(II)设直线l的方程为:y=2x+b,
故有过AB的直线的方程为y=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
由A、B是抛物线上不同的两点,于是上述方程的判别式△=
| 1 |
| 4 |
| 1 |
| 32 |
由直线AB的中点为(
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
| 1 |
| 8 |
| 1 |
| 16 |
则
| 1 |
| 16 |
| 1 |
| 4 |
| 5 |
| 16 |
| 5 |
| 16 |
| 1 |
| 32 |
| 9 |
| 32 |
即得l在y轴上的截距的取值范围是(
| 9 |
| 32 |

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
 中,已知抛物线
中,已知抛物线 :
: ,在此抛物线上一点
,在此抛物线上一点
 到焦点的距离是3.
到焦点的距离是3. 轴交于
轴交于 的直线
的直线 与抛物线
与抛物线 、
、 两点.是否存在这样的
两点.是否存在这样的 满足
满足 ,若存在,求
,若存在,求
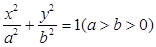 经过点
经过点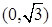 ,离心率为
,离心率为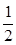 ,左右焦点分别为
,左右焦点分别为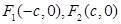 .
.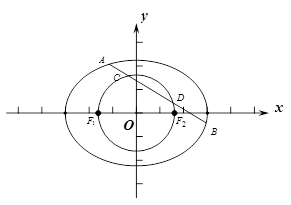
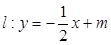 与椭圆交于
与椭圆交于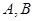 两点,与以
两点,与以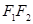 为直径的圆交于
为直径的圆交于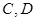 两点,且满足
两点,且满足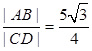 ,求直线
,求直线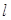 的方程.
的方程.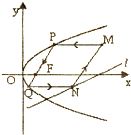
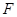 为抛物线
为抛物线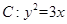 的焦点,过
的焦点,过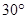 的直线交
的直线交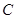 于
于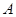 ,
,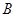 两点,则
两点,则 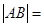 ( )
( )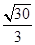
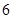
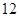
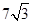
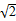 的圆C与直线y=x相切于坐标原点O,椭圆
的圆C与直线y=x相切于坐标原点O,椭圆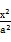 +
+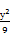 =1与圆C的一个交点到椭圆两焦点的距离之和为10.
=1与圆C的一个交点到椭圆两焦点的距离之和为10.