题目内容
(本题满分10分) 如图,在平行四边形 中,
中, ,将
,将 沿
沿 折起到
折起到 的位置,使平面
的位置,使平面 平面
平面 .
.
(1)求二面角E-AB-D的大小;
(2)求四面体 的表面积和体积.
的表面积和体积.
(1)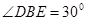 (或证
(或证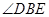 即为
即为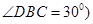 .(2)
.(2)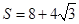 ,V=
,V=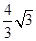
解析试题分析:(1)在 中,
中,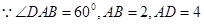 ,
, ,
,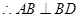 因为平面
因为平面 平面
平面 ,所以
,所以 平面
平面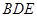 ,
, .
.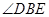 即为二面角
即为二面角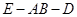 的平面角.
的平面角.
解三角形得到。
(2)在第一问的基础上,进一步得到体高,和边长,求解表面积和体积。
(1)在 中,
中,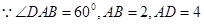 ,
, .
. ,
,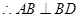
因为平面 平面
平面 ,所以
,所以 平面
平面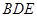 ,
, .
.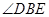 即为二面角
即为二面角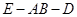 的平面角.
的平面角.
又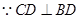 ,
,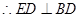 ,而
,而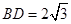 ,
,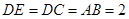 ,
,
故在直角三角形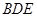 中,
中,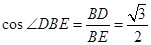 ,
,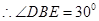 (或证
(或证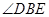 即为
即为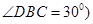 .
.
(2)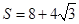 ,V=
,V=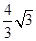
考点:本题主要是考查二面角的平面角的求解,以及四面体的表面积和体积的运算问题。
点评:解决该试题的关键是利用三垂线定理作出二面角的平面角,以及利用特殊三角形的面积得到表面积和四面体体积。

练习册系列答案
相关题目
 B
B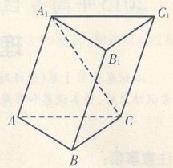

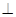 平面PBD;
平面PBD;
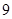 m,
m,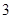 m.某广告公司计划在此空地上竖一块长方形液晶广告屏幕
m.某广告公司计划在此空地上竖一块长方形液晶广告屏幕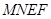 ,
,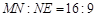 .线段MN必须过点P,端点M,N分别在边AD,AB上,设AN=x(m),液晶广告屏幕MNEF的面积为S(m2).
.线段MN必须过点P,端点M,N分别在边AD,AB上,设AN=x(m),液晶广告屏幕MNEF的面积为S(m2).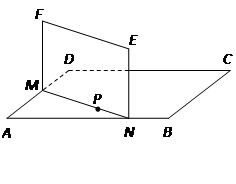
 、
、 分别是
分别是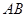 、
、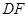 的中点.
的中点.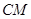
 平面
平面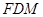
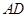 上(含
上(含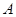 、
、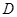 端点)确定一点
端点)确定一点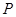 ,使得
,使得
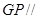 平面
平面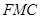 ,并给出证明;
,并给出证明;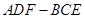 内自由飞,求它飞入几何体
内自由飞,求它飞入几何体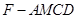 内的概率.
内的概率. 
 三点处,
三点处,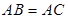 ,
,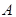 到线段
到线段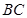 的距离
的距离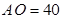 ,
,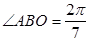 (参考数据:
(参考数据: 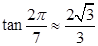 ). 今计划建一个生活垃圾中转站
). 今计划建一个生活垃圾中转站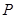 ,为方便运输,
,为方便运输,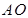 (不含端点)上.
(不含端点)上.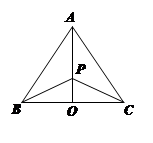
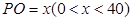 ,试将
,试将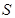 表示为
表示为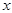 的函数,并求
的函数,并求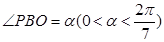 ,试将
,试将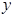 表示为
表示为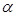 的函数,并确定当
的函数,并确定当 中,若
中,若 ,
,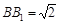 ,
, 是
是 中点。
中点。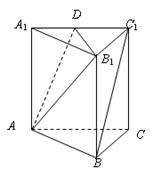
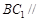 平面
平面 ;
; 与
与 所成的角的大小。
所成的角的大小。 ,求这个圆台的侧面积.
,求这个圆台的侧面积.