题目内容
(14分)如图,ABCD是正方形空地,边长为30m,电源在点P处,点P到边AD,AB距离分别为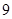 m,
m,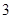 m.某广告公司计划在此空地上竖一块长方形液晶广告屏幕
m.某广告公司计划在此空地上竖一块长方形液晶广告屏幕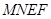 ,
,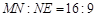 .线段MN必须过点P,端点M,N分别在边AD,AB上,设AN=x(m),液晶广告屏幕MNEF的面积为S(m2).
.线段MN必须过点P,端点M,N分别在边AD,AB上,设AN=x(m),液晶广告屏幕MNEF的面积为S(m2).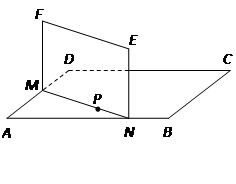
(1)求S关于x的函数关系式及该函数的定义域;
(2)当x取何值时,液晶广告屏幕MNEF的面积S最小?
(1) 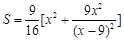 ,定义域为
,定义域为 .(2)当AN长为
.(2)当AN长为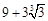 m时,液晶广告屏幕
m时,液晶广告屏幕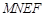 的面积
的面积 最小.
最小.
解析试题分析:解:(1)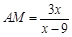
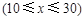 . …………………………………2分
. …………………………………2分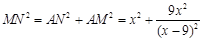 . ……………………4分
. ……………………4分
∵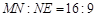 , ∴
, ∴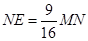 .
.
∴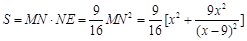 . …………………6分
. …………………6分
定义域为 . ……………………………7分
. ……………………………7分
(2)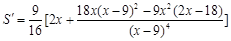 =
=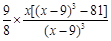 , …9分
, …9分
令 ,得
,得 (舍),
(舍),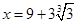 . …………………10分
. …………………10分
当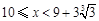 时,
时,
 关于
关于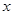 为减函数;
为减函数;
当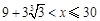 时,
时,
 关于
关于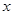 为增函数;
为增函数;
∴当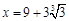 时,
时, 取得最小值. ……………13分
取得最小值. ……………13分
答:当AN长为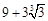 m时,液晶广告屏幕
m时,液晶广告屏幕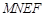 的面积
的面积 最小.……14分
最小.……14分
考点:函数的应用题;生活中的优化问题;导数的实际应用。
点评:研究数学模型,建立数学模型,进而借鉴数学模型,对提高解决实际问题的能力,以及提高数学素养都是十分重要的.建立模型的步骤可分为: (1) 分析问题中哪些是变量,哪些是常量,分别用字母表示; (2) 根据所给条件,运用数学知识,确定等量关系; (3) 写出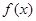 的解析式并指明定义域。
的解析式并指明定义域。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
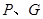 分别是
分别是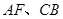 中点
中点
 .
. ,且
,且 ,
, 分别为
分别为 、
、 、
、 的中点
的中点
 的大小为
的大小为 ?若存在,求出CQ的长;若不存在,请说明理由。
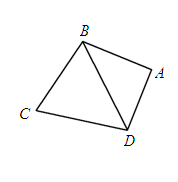
?若存在,求出CQ的长;若不存在,请说明理由。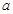 ,BC=CD=BD,设
,BC=CD=BD,设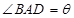 .
.
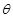 的函数;
的函数;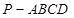 的侧面
的侧面 垂直于底面
垂直于底面 ,
,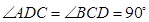
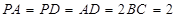 ,
,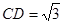 ,
, 在棱
在棱 上,
上,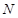 是
是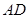 的中点,二面角
的中点,二面角 为
为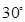 求
求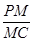 的值;
的值;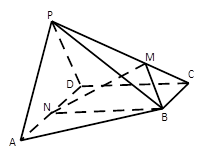
 中,
中, ,将
,将 沿
沿 折起到
折起到 的位置,使平面
的位置,使平面 平面
平面 .
. 的表面积和体积.
的表面积和体积.
 中,
中, ,
, ,
, 为
为 的中点。
的中点。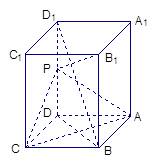
 ∥平面
∥平面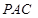 ;
;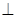 平面
平面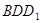 ;
;
 时,有DN ∥平面AEM,求
时,有DN ∥平面AEM,求  的值;
的值;
 中,
中, 是正三角形,
是正三角形, ,
, .
.  表示成关于
表示成关于 的函数;
的函数;