题目内容
(本小题满分12分)
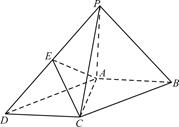
如图,在底面为平行四边形的四棱锥P—ABCD中,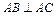 ,
,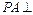 平面
平面 ,且
,且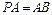 ,点E是PD的中点.
,点E是PD的中点.
(1)证明: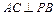 ;
;
(2)证明: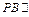 平面AEC;
平面AEC;
(3)求二面角E—AC—B的大小.

如图,在底面为平行四边形的四棱锥P—ABCD中,
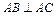 ,
,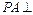 平面
平面 ,且
,且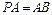 ,点E是PD的中点.
,点E是PD的中点.(1)证明:
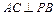 ;
;(2)证明:
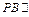 平面AEC;
平面AEC;(3)求二面角E—AC—B的大小.
(1)因AB是PB在平面ABCD的射影,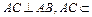 平面ABCD,故
平面ABCD,故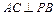 (4分)
(4分)
(2)连BD交AC于O,连EO,易知BO=DO,PE=DE,故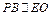 ,
,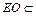 平面AEC,
平面AEC,
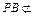 平面AEC,故
平面AEC,故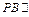 平面AEC (8分)
平面AEC (8分)
(3)取AD中点F,连EF,FO,则易知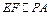 ,
,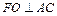 ,故
,故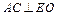 ,故∠EOF为二面角
,故∠EOF为二面角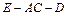 的平面角,又
的平面角,又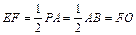 ,故
,故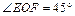 ,而二面角
,而二面角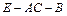 与二面角
与二面角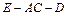 互补,故二面角
互补,故二面角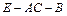 的平面角为
的平面角为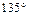 (12分)
(12分)
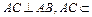 平面ABCD,故
平面ABCD,故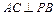 (4分)
(4分)(2)连BD交AC于O,连EO,易知BO=DO,PE=DE,故
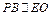 ,
,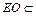 平面AEC,
平面AEC,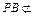 平面AEC,故
平面AEC,故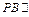 平面AEC (8分)
平面AEC (8分)(3)取AD中点F,连EF,FO,则易知
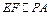 ,
,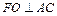 ,故
,故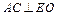 ,故∠EOF为二面角
,故∠EOF为二面角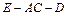 的平面角,又
的平面角,又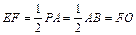 ,故
,故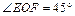 ,而二面角
,而二面角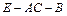 与二面角
与二面角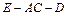 互补,故二面角
互补,故二面角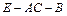 的平面角为
的平面角为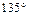 (12分)
(12分)略

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
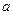 ,D为BC中点,M在BB1上,且
,D为BC中点,M在BB1上,且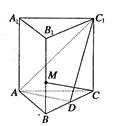
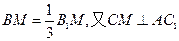 .
.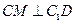 ;
;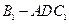 的体积.
的体积.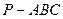 中,
中,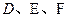 分别是
分别是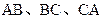 的中点,下面四个结论中不成立的是
的中点,下面四个结论中不成立的是 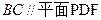
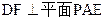
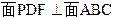
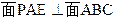
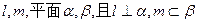 ,给出下列四个命题
,给出下列四个命题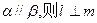 ;②若
;②若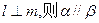 ;③若
;③若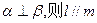 ;④若
;④若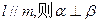
 和两条异面直线都平行的直线(
和两条异面直线都平行的直线(  )
)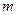 、
、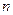 ,平面
,平面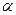 、
、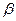 ,给出下列命题:
,给出下列命题:
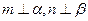 ,且
,且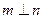 ,则
,则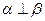 ②若
②若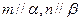 ,且
,且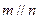 ,则
,则
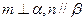 ,且
,且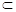 α,则l∥β
α,则l∥β