Question

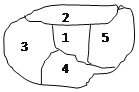
【题目】如图所示四棱锥中，底面，四边形中，，，，．

求四棱锥的体积；

求证：平面；

在棱上是否存在点异于点，使得平面，若存在，求的值；若不存在，说明理由．

Answer 1

【答案】（1）4；（2）见解析；（3）不存在.

【解析】

利用四边形是直角梯形，求出，结合底面，利用棱锥的体积公式求解即可求；先证明，，结合，利用线面垂直的判定定理可得平面 ；用反证法证明，假设存在点异于点使得平面证明平面平面，与平面与平面相交相矛盾，从而可得结论．

显然四边形ABCD是直角梯形，

又底面

平面ABCD，平面ABCD，

在直角梯形ABCD中，，

，，即

又，

平面；

不存在，下面用反证法进行证明

假设存在点异于点使得平面PAD．

，且平面PAD，

平面PAD，

平面PAD

又，

平面平面PAD

而平面PBC与平面PAD相交，得出矛盾．