题目内容
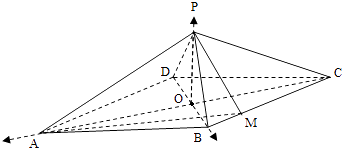
【题目】如图,四棱锥P﹣ABCD,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD= ![]() ,M为BC上的一点,且BM=
,M为BC上的一点,且BM= ![]() ,MP⊥AP.
,MP⊥AP. 
(1)求PO的长;
(2)求二面角A﹣PM﹣C的正弦值.
【答案】
(1)解:连接AC,BD,
∵底面是以O为中心的菱形,PO⊥底面ABCD,
故AC∩BD=O,且AC⊥BD,
以O为坐标原点,OA,OB,OP方向为x,y,z轴正方向建立空间坐标系O﹣xyz,
∵AB=2,∠BAD= ![]() ,
,
∴OA=ABcos( ![]() ∠BAD)=
∠BAD)= ![]() ,OB=ABsin(
,OB=ABsin( ![]() ∠BAD)=1,
∠BAD)=1,
∴O(0,0,0),A( ![]() ,0,0),B(0,1,0),C(﹣
,0,0),B(0,1,0),C(﹣ ![]() ,0,0),
,0,0),
![]() =(0,1,0),
=(0,1,0), ![]() =(﹣
=(﹣ ![]() ,﹣1,0),
,﹣1,0),
又∵BM= ![]() ,
,
∴ ![]()
![]() =(﹣
=(﹣ ![]() ,﹣
,﹣ ![]() ,0),
,0),
则 ![]() =
= ![]() +
+ ![]() =(﹣
=(﹣ ![]() ,
, ![]() ,0),
,0),
设P(0,0,a),则 ![]() =(﹣
=(﹣ ![]() ,0,a),
,0,a), ![]() =(
=( ![]() ,﹣
,﹣ ![]() ,a),
,a),
∵MP⊥AP,
∴ ![]()
![]() =
= ![]() ﹣a2=0,
﹣a2=0,
解得a= ![]() ,
,
即PO的长为 ![]() .
.
(2)解:由(1)知 ![]() =(﹣
=(﹣ ![]() ,0,
,0, ![]() ),
), ![]() =(
=( ![]() ,﹣
,﹣ ![]() ,
, ![]() ),
), ![]() =(
=( ![]() ,0,
,0, ![]() ),
),
设平面APM的法向量 ![]() =(x,y,z),平面PMC的法向量为
=(x,y,z),平面PMC的法向量为 ![]() =(a,b,c),
=(a,b,c),
由  ,得
,得 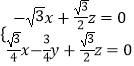 ,
,
令x=1,则 ![]() =(1,
=(1, ![]() ,2),
,2),
由 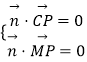 ,得
,得 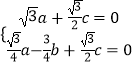 ,
,
令a=1,则 ![]() =(1,﹣
=(1,﹣ ![]() ,﹣2),
,﹣2),
∵平面APM的法向量 ![]() 和平面PMC的法向量
和平面PMC的法向量 ![]() 夹角θ满足:
夹角θ满足:
cosθ= ![]() =
= ![]() =﹣
=﹣ ![]()
故sinθ= ![]() =
= ![]()
【解析】(1)连接AC,BD,以O为坐标原点,OA,OB,OP方向为x,y,z轴正方向建立空间坐标系O﹣xyz,分别求出向量 ![]() ,
, ![]() 的坐标,进而根据MP⊥AP,得到
的坐标,进而根据MP⊥AP,得到 ![]()
![]() =0,进而求出PO的长;(2)求出平面APM和平面PMC的法向量,代入向量夹角公式,求出二面角的余弦值,进而根据平方关系可得:二面角A﹣PM﹣C的正弦值
=0,进而求出PO的长;(2)求出平面APM和平面PMC的法向量,代入向量夹角公式,求出二面角的余弦值,进而根据平方关系可得:二面角A﹣PM﹣C的正弦值

【题目】2015男篮亚锦赛决赛阶段,中国男篮以9连胜的不败战绩赢得第28届亚锦赛冠军,同时拿到亚洲唯一1张直通里约奥运会的入场券.赛后,中国男篮主力易建联荣膺本届亚锦赛MVP(最有价值球员),下表是易建联在这9场比赛中投篮的统计数据.
比分 | 易建联技术统计 | |||
投篮命中 | 罚球命中 | 全场得分 | 真实得分率 | |
中国91﹣42新加坡 | 3/7 | 6/7 | 12 | 59.52% |
中国76﹣73韩国 | 7/13 | 6/8 | 20 | 60.53% |
中国84﹣67约旦 | 12/20 | 2/5 | 26 | 58.56% |
中国75﹣62哈萨克期坦 | 5/7 | 5/5 | 15 | 81.52% |
中国90﹣72黎巴嫩 | 7/11 | 5/5 | 19 | 71.97% |
中国85﹣69卡塔尔 | 4/10 | 4/4 | 13 | 55.27% |
中国104﹣58印度 | 8/12 | 5/5 | 21 | 73.94% |
中国70﹣57伊朗 | 5/10 | 2/4 | 13 | 55.27% |
中国78﹣67菲律宾 | 4/14 | 3/6 | 11 | 33.05% |
注:(1)表中a/b表示出手b次命中a次;
(2)TS%(真实得分率)是衡量球员进攻的效率,其计算公式为:
TS%=.全场得分/2x(投篮出手次数+0.44x罚球出手次数)
(Ⅰ)从上述9场比赛中随机选择一场,求易建联在该场比赛中TS%超过50%的概率;
(Ⅱ)从上述9场比赛中随机选择两场,求易建联在这两场比赛中TS%至少有一场超过60%的概率;
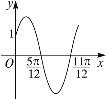
(Ⅲ)用x来表示易建联某场的得分,用y来表示中国队该场的总分,画出散点图如图所示,请根据散点图判断y与x之间是否具有线性相关关系?结合实际简单说明理由.
【题目】高二学生小严利用暑假参加社会实践,为了帮助贸易公司的购物网站优化今年国庆节期间的营销策略,他对去年10月1日当天在该网站消费且消费金额不超过1000元的1000名(女性800名,男性200名)网购者,根据性别按分层抽样的方法抽取100名进行分析,得到如下统计图表(消费金额单位:元):
女性消费情况:
消费金额 | (0,200) | [200,400) | [400,600) | [600,800) | [800,1000) |
人数 | 5 | 10 | 15 |
|
|
男性消费情况:
消费金额 | (0,200) | [200,400) | [400,600) | [600,800) | [800,1000) |
人数 | 2 | 3 | 10 |
| 2 |
(1)现从抽取的100名且消费金额在[800,1000](单位:元)的网购者中随机选出两名发放网购红包,求选出的这两名网购者恰好是一男一女的概率;
(2)若消费金额不低于600元的网购者为“网购达人”,低于600元的网购者为“非网购达人”,根据以上统计数据填写下面![]() 列联表,并回答能否在犯错误的概率不超过0.010的前提下认为“是否为‘网购达人’与性别有关?”
列联表,并回答能否在犯错误的概率不超过0.010的前提下认为“是否为‘网购达人’与性别有关?”
女性 | 男性 | 总计 | |
网购达人 | |||
非网购达人 | |||
总计 |
附:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
(![]() ,其中
,其中![]() )
)
【题目】某二手车交易市场对某型号的二手汽车的使用年数![]() 与销售价格
与销售价格![]() (单位:万元/辆)进行整理,得到如下的对应数据:
(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
售价 | 16 | 13 | 9.5 | 7 | 4.5 |
(1)试求![]() 关于
关于![]() 的回归直线方程:(参考公式:
的回归直线方程:(参考公式: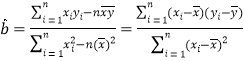 ,
, ![]() .)
.)
(2)已知每辆该型号汽车的收购价格为![]() 万元,根据(1)中所求的回归方程,预测
万元,根据(1)中所求的回归方程,预测![]() 为何值时,销售一辆该型号汽车所获得的利润
为何值时,销售一辆该型号汽车所获得的利润![]() 最大?
最大?