题目内容
【题目】某学校要对如图所示的5个区域进行绿化(种花),现有4种不同颜色的花供选择,要求相邻区域不能种同一种颜色的花,则共有___________种不同的种花方法.
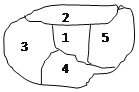
【答案】72
【解析】分析: 根据题意,分4步进行分析:依次分析区域1、2、3、4和5的着色方法数目,由分步计数原理计算可得答案.
详解:根据题意,分4步进行分析:
①,对于区域1,有4种颜色可选,即有4种着色方法,
②,对于区域2,与区域1相邻,有3种颜色可选,即有3种着色方法,
③,对于区域3,与区域1、2相邻,有2种颜色可选,即有2种着色方法,
④,对于区域4,若其颜色与区域2的相同,区域5有2种颜色可选,
若其颜色与区域2的不同,区域4有1种颜色可选,区域5有1种颜色可选,
则区域4、5共有2+1=3种着色方法;
则一共有4×3×2×(1+2)=72种着色方法;
故答案为:72

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目