题目内容
16.一个不透明的盒子中装有4个完全相同的小球,球上分别编有数字1、2、3、4.(1)若逐个不放回取球两次,求第一次取到球的编号为偶数且两个球的编号之和能被3整除的概率;
(2)若先从盒中随机取一个球,该球的编号为a,将球放回盒中,然后再从盒中随机取一个球,该球的编号为b.
①求使得函数f(x)=asinx+bcosx的最大值小于4的概率;
②求使得向量$\overrightarrow{m}$=(2a-6,2)与$\overrightarrow{n}$=(3-2b,-1)夹角为钝角的概率.
分析 (1)从逐个不放回取球两次,共有4×3=12种,第一次取到球的编号为偶数且两个球的编号之和能被3整除的有(2,1),(2,4),(4,2)3种,根据概率公式计算即可;
(2)先从盒中随机取一个球,该球的编号为a,将球放回盒中,然后再从盒中随机取一个球,该球的编号为b.共有4×4=16种,
①其中函数f(x)=asinx+bcosx的最大值大于等于4的只有一种,根据概率公式计算即可;
②其中使得向量$\overrightarrow{m}$=(2a-6,2)与$\overrightarrow{n}$=(3-2b,-1)夹角为钝角有10种,根据概率公式计算即可.
解答 解:(1)从逐个不放回取球两次,共有4×3=12种,分别为(1,2),(2,1),(1,3),(3,1),(1,4),(4,1),(2,3),(3,2),(2,4),(4,2),(3,4),(4,3),第一次取到球的编号为偶数且两个球的编号之和能被3整除的有(2,1),(2,4),(4,2)3种,
故第一次取到球的编号为偶数且两个球的编号之和能被3整除的概率为$\frac{3}{12}$=$\frac{1}{4}$.
(2)先从盒中随机取一个球,该球的编号为a,将球放回盒中,然后再从盒中随机取一个球,该球的编号为b.共有4×4=16种,分别为(1,1),(2,2),(3,3),(4,4),(1,2),(2,1),(1,3),(3,1),(1,4),(4,1),(2,3),(3,2),(2,4),(4,2),(3,4),(4,3),
①∵函数f(x)=asinx+bcosx=$\sqrt{{a}^{2}+{b}^{2}}$sin(x+θ),
∴函数f(x)=asinx+bcosx的最大值为$\sqrt{{a}^{2}+{b}^{2}}$,
∴$\sqrt{{a}^{2}+{b}^{2}}$<4,
即a2+b2<16,因为只有42+42=16,其它均小于16,
故函数f(x)=asinx+bcosx的最大值小于4的概率P=1-$\frac{1}{16}$=$\frac{15}{16}$.
②∵向量$\overrightarrow{m}$=(2a-6,2)与$\overrightarrow{n}$=(3-2b,-1)夹角为钝角,
∴(2a-6)(3-2b)+2×(-1)<0,
即(a-3)(3-2b)<2,
共有(1,1),(2,1),(3,1),(4,1),(2,2),(3,2),(4,2),(4,3),(4,4),(3,4)共10种,
故向量$\overrightarrow{m}$=(2a-6,2)与$\overrightarrow{n}$=(3-2b,-1)夹角为钝角的概率为$\frac{10}{16}$=$\frac{5}{8}$.
点评 本题考查了古典概型的概率问题,关键是列举出所有满足条件的基本事件,属于中档题.

| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
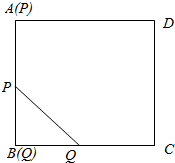 如图,正方形ABCD的边长为1,点P从顶点A沿着A→B的方向向顶点B运动,速度为2,同时,点Q从顶点B沿着B→C方向向顶点C运动,速度为1,则|PQ|的最小值为( )
如图,正方形ABCD的边长为1,点P从顶点A沿着A→B的方向向顶点B运动,速度为2,同时,点Q从顶点B沿着B→C方向向顶点C运动,速度为1,则|PQ|的最小值为( )| A. | 0 | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 1 |
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{2}$ | D. | 2 |
| A. | (n-1)•2n+1 | B. | $\frac{n+2}{{2}^{n-1}}$-2 | C. | $\frac{2-n}{{2}^{n-1}}$ | D. | 4-$\frac{n+2}{{2}^{n-1}}$ |