题目内容
如图,三棱柱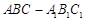 中,
中,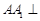 面
面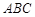 ,
,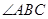 =
=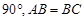 ,
,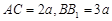 ,
, 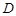 为
为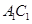 的中点,
的中点,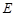 为
为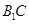 的中点:
的中点:
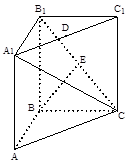
(1)求直线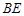 与
与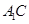 所成的角的余弦值;
所成的角的余弦值;
(2)在线段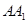 上是否存在点
上是否存在点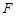 ,使
,使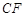
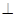 平面
平面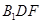 ,若存在,求出
,若存在,求出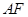 ;若不存在,说明理由。
;若不存在,说明理由。
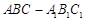 中,
中,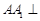 面
面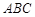 ,
,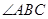 =
=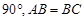 ,
,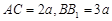 ,
, 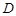 为
为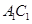 的中点,
的中点,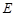 为
为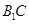 的中点:
的中点: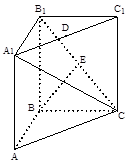
(1)求直线
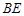 与
与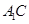 所成的角的余弦值;
所成的角的余弦值;(2)在线段
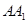 上是否存在点
上是否存在点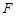 ,使
,使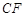
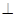 平面
平面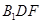 ,若存在,求出
,若存在,求出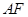 ;若不存在,说明理由。
;若不存在,说明理由。(1).以B为原点,BA、BC、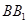 所在直线分别为x,y,z轴建立空间直角坐标系,
所在直线分别为x,y,z轴建立空间直角坐标系,
因为AC=2a,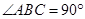 ,所以AB =BC=
,所以AB =BC= a所以B(0,0,0),C(0,
a所以B(0,0,0),C(0, a,0),
a,0),
A( a,0,0),
a,0,0),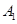 (
( a,0,3a),
a,0,3a), ( 0,
( 0, a,3a),
a,3a), 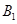 (0,0,3a),D(
(0,0,3a),D( ),E(
),E( )
)
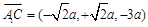 ,
,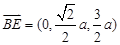 ,则cos<
,则cos<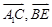 >=
>=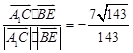
所以直线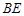 与
与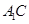 所成的角的余弦值
所成的角的余弦值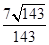
 -----------6分
-----------6分
(2)假设存在点F,使CF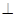 平面
平面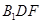 ,不妨设AF=b,则F(
,不妨设AF=b,则F( ),
),
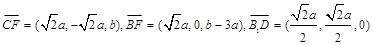 ----------9分
----------9分
所以 解之得b=a或b=2a,
解之得b=a或b=2a,
所以当AF=a或2a时,CF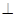 平面
平面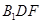
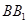 所在直线分别为x,y,z轴建立空间直角坐标系,
所在直线分别为x,y,z轴建立空间直角坐标系,因为AC=2a,
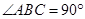 ,所以AB =BC=
,所以AB =BC= a所以B(0,0,0),C(0,
a所以B(0,0,0),C(0, a,0),
a,0),A(
 a,0,0),
a,0,0),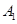 (
( a,0,3a),
a,0,3a), ( 0,
( 0, a,3a),
a,3a), 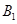 (0,0,3a),D(
(0,0,3a),D( ),E(
),E( )
)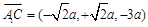 ,
,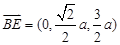 ,则cos<
,则cos<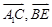 >=
>=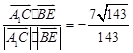
所以直线
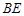 与
与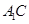 所成的角的余弦值
所成的角的余弦值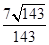
 -----------6分
-----------6分(2)假设存在点F,使CF
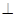 平面
平面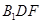 ,不妨设AF=b,则F(
,不妨设AF=b,则F( ),
),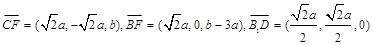 ----------9分
----------9分所以
 解之得b=a或b=2a,
解之得b=a或b=2a,所以当AF=a或2a时,CF
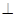 平面
平面
略

练习册系列答案
相关题目
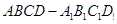 中,
中,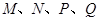 分别是
分别是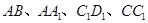 的中点,给出以下四个结论:
的中点,给出以下四个结论: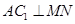 ; ②
; ②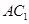 //平面
//平面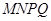 ; ③
; ③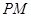 相交; ④
相交; ④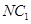 与
与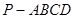 中,底面是边长为
中,底面是边长为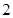 的正方形,侧棱
的正方形,侧棱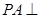 底面
底面 ,
,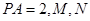 分别为
分别为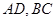 的中点.
的中点.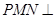 平面
平面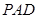 ;
;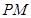 与平面
与平面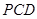 所成角的正弦值;
所成角的正弦值;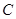 到平面
到平面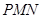 的距离.
的距离.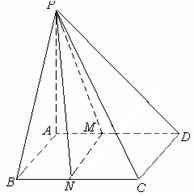
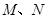 分别是
分别是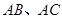 的中点,
的中点,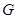 是
是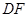 上的一动点.
上的一动点.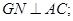
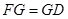 时,在棱
时,在棱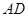 上确定一点
上确定一点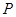 ,使得
,使得 //平面
//平面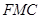 ,并给出证明.
,并给出证明. 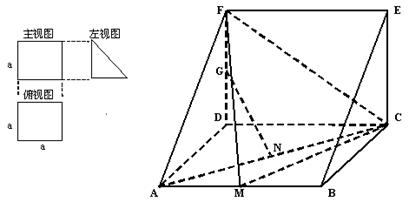
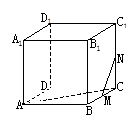
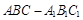 的直观图和三视图如图所示(主视图、俯视图都是矩形,左视图是直角三角形),设
的直观图和三视图如图所示(主视图、俯视图都是矩形,左视图是直角三角形),设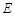 为线段
为线段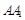 上的点.
上的点. 的体积;
的体积; 平面
平面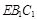 ,若存在,求AE的长.
,若存在,求AE的长.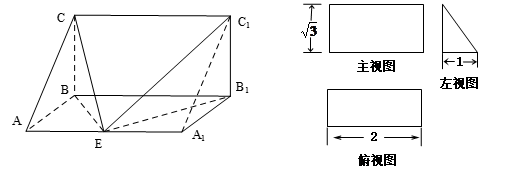
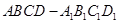 的棱长为2,
的棱长为2,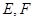 分别是
分别是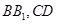 的中点.
的中点. 的体积;
的体积;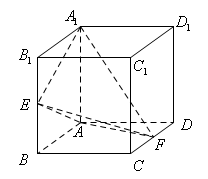
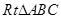 中,
中,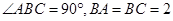 ,分别过
,分别过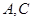 作平面
作平面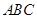 的垂线
的垂线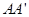 和
和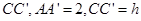 ,连结
,连结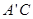 和
和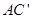 交于点
交于点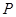 .
.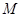 为
为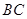 中点,若
中点,若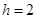 ,求证:直线
,求证:直线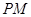 与平面
与平面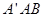 平行;
平行;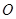 为
为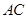
 中点,二面角
中点,二面角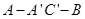 等于
等于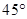 ,求直线
,求直线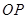 与平面
与平面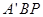 所成角
所成角