题目内容
【题目】如图,在三棱柱![]() 中,
中,![]() 底面
底面![]() ,△ABC是边长为
,△ABC是边长为![]() 的正三角形,
的正三角形,![]() ,D,E分别为AB,BC的中点.
,D,E分别为AB,BC的中点.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)在线段![]() 上是否存在一点M,使
上是否存在一点M,使![]() 平面
平面![]() ?说明理由.
?说明理由.
【答案】(Ⅰ)见证明;(Ⅱ) ![]() (Ⅲ)见解析
(Ⅲ)见解析
【解析】
(Ⅰ)推导出AA1⊥CD,CD⊥AB,由此能证明CD⊥平面AA1B1B.
(Ⅱ)取A1B1中点F,连结DF,如图空间直角坐标系D﹣xyz,利用向量法能求出二面角B﹣AE﹣B1的余弦值.
(Ⅲ)假设线段B1C1上存在点M,使BM⊥平面AB1E.则λ∈[0,1],使得![]() .求出平面AB1法向量,利用向量法能求出在线段B1C1上不存在点M,使BM⊥平面AB1E.
.求出平面AB1法向量,利用向量法能求出在线段B1C1上不存在点M,使BM⊥平面AB1E.
(Ⅰ)证明:在三棱柱![]() 中,
中,
因为![]() 底面
底面![]() ,CD平面ABC,
,CD平面ABC,
所以![]() .
.
又![]() 为等边三角形,
为等边三角形,![]() 为
为![]() 的中点,
的中点,
所以![]() .因为
.因为![]() ,
,
所以![]() 平面
平面![]() ;
;
(Ⅱ)取![]() 中点
中点![]() ,连结
,连结![]() ,则
,则
因为![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,
所以![]() .
.
由(Ⅰ)知![]() ,
,![]() ,
,
如图建立空间直角坐标系![]() .
.
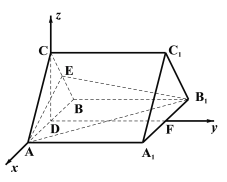
由题意得![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
设平面![]()
![]() 法向量
法向量![]() ,
,![]()
则 即
即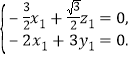
令![]() ,则
,则![]() ,
,![]() .即
.即![]() .
.
平面BAE法向量![]() .
.
因为![]() ,
,![]() ,
,![]() ,
,
所以
由题意知二面角![]() 为锐角,所以它的余弦值为
为锐角,所以它的余弦值为![]() .
.
(Ⅲ)解:在线段![]() 上不存在点M,使
上不存在点M,使![]() 平面
平面![]() .理由如下.
.理由如下.
假设线段![]() 上存在点M,使
上存在点M,使![]() 平面
平面![]() .则
.则
![]() ,使得
,使得![]() .
.
因为![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() .
.
由(Ⅱ)可知,平面![]() 法向量
法向量![]() ,
,
![]() 平面
平面![]() ,当且仅当
,当且仅当![]() ,
,
即![]() ,使得
,使得![]() .
.
所以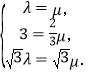 解得
解得![]() .
.
这与![]() 矛盾.
矛盾.
所以在线段![]() 上不存在点M,使
上不存在点M,使![]() 平面
平面![]() .
.

 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案【题目】北京地铁八通线西起四惠站,东至土桥站,全长18.964km,共设13座车站.目前八通线执行2014年12月28日制订的计价标准,各站间计程票价(单位:元)如下:
四惠 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | |
四惠东 | 3 | 3 | 3 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | ||
高碑店 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 | p>5 | |||
传媒大学 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 | ||||
双桥 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | |||||
管庄 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | ||||||
八里桥 | 3 | 3 | 3 | 3 | 4 | 4 | |||||||
通州北苑 | 3 | 3 | 3 | 3 | 3 | ||||||||
果园 | 3 | 3 | 3 | 3 | |||||||||
九棵树 | 3 | 3 | 3 | ||||||||||
梨园 | /p> | 3 | 3 | ||||||||||
临河里 | 3 | ||||||||||||
土桥 | |||||||||||||
四惠 | 四惠东 | 高碑店 | 传媒大学 | 双桥 | 管庄 | 八里桥 | 通州北苑 | 果园 | 九棵树 | 梨园 | 临河里 | 土桥 |
(Ⅰ)在13座车站中任选两个不同的车站,求两站间票价不足5元的概率;
(Ⅱ)甲乙二人从四惠站上车乘坐八通线,各自任选另一站下车(二人可同站下车),记甲乙二人乘车购票花费之和为X元,求X的分布列;
(Ⅲ)若甲乙二人只乘坐八通线,甲从四惠站上车,任选另一站下车,记票价为![]() 元;乙从土桥站上车,任选另一站下车,记票价为
元;乙从土桥站上车,任选另一站下车,记票价为![]() 元.试比较
元.试比较![]() 和
和![]() 的方差
的方差![]() 和
和![]() 大小.(结论不需要证明)
大小.(结论不需要证明)
【题目】2020年寒假是特殊的寒假,因为抗击疫情全体学生只能在家进行网上在线学习,为了研究学生在网上学习的情况,某学校在网上随机抽取120名学生对线上教育进行调查,其中男生与女生的人数之比为11:13,其中男生30人对于线上教育满意,女生中有15名表示对线上教育不满意.
(1)完成![]() 列联表,并回答能否有99%的把握认为对“线上教育是否满意与性别有关”;
列联表,并回答能否有99%的把握认为对“线上教育是否满意与性别有关”;
满意 | 不满意 | 总计 | |
男生 | 20 | ||
女生 | 15 | ||
合计 | 120 |
(2)从被调查的对线上教育满意的学生中,利用分层抽样抽取8名学生,再在8名学生中抽取3名学生,作线上学习的经验介绍,其中抽取男生的个数为![]() ,求出
,求出![]() 的分布列及期望值.
的分布列及期望值.
参考公式:附:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 0.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10828 |