题目内容
【题目】设椭圆![]() 的右顶点为A,下顶点为B,过A、O、B(O为坐标原点)三点的圆的圆心坐标为
的右顶点为A,下顶点为B,过A、O、B(O为坐标原点)三点的圆的圆心坐标为![]() .
.
(1)求椭圆的方程;
(2)已知点M在x轴正半轴上,过点B作BM的垂线与椭圆交于另一点N,若∠BMN=60°,求点M的坐标.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)根据直径所对圆周角为直角可知![]() 为直径,根据圆心坐标求得
为直径,根据圆心坐标求得![]() 的值进而求得椭圆的方程.(2)由(1)求得
的值进而求得椭圆的方程.(2)由(1)求得![]() 点的坐标,设出直线
点的坐标,设出直线![]() 的方程,同时得到直线
的方程,同时得到直线![]() 的方程.联立直线
的方程.联立直线![]() 的方程和椭圆方程,解出
的方程和椭圆方程,解出![]() 点的坐标,由此求得
点的坐标,由此求得![]() 的表达式.通过直线
的表达式.通过直线![]() 的方程求得
的方程求得![]() 点的坐标,进而求得
点的坐标,进而求得![]() 的表达式,利用
的表达式,利用![]() 得到
得到![]() ,由此列方程解得
,由此列方程解得![]() 的值,从而求得
的值,从而求得![]() 点的坐标.
点的坐标.
解:(1)依题意知![]() ,
,![]() ,
,
∵△AOB为直角三角形,∴过A、O、B三点的圆的圆心为斜边AB的中点,
∴![]() ,即
,即![]() ,
,
∴椭圆的方程为![]() .
.
(2)由(1)知![]() ,依题意知直线BN的斜率存在且小于0,
,依题意知直线BN的斜率存在且小于0,
设直线BN的方程为![]() ,
,
则直线BM的方程为:![]() ,
,
由![]() 消去y得
消去y得![]() ,
,
解得:![]() ,
,![]() ,
,
∴![]()
![]()
∴![]()
![]() ,
,
在![]() 中,令
中,令![]() 得
得![]() ,即
,即![]()
∴![]() ,
,
在Rt△MBN中,∵∠BMN=60°,∴![]() ,
,
即![]() ,整理得
,整理得![]() ,
,
解得![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
∴点M的坐标为![]() .
.

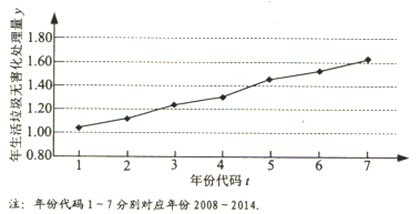
【题目】某县畜牧技术员张三和李四9年来一直对该县山羊养殖业的规模进行跟踪调查,张三提供了该县某山羊养殖场年养殖数量![]() (单位:万只)与相应年份
(单位:万只)与相应年份![]() (序号)的数据表和散点图(如图所示),根据散点图,发现
(序号)的数据表和散点图(如图所示),根据散点图,发现![]() 与
与![]() 有较强的线性相关关系,李四提供了该县山羊养殖场的个数
有较强的线性相关关系,李四提供了该县山羊养殖场的个数![]() (单位:个)关于
(单位:个)关于![]() 的回归方程
的回归方程![]() .
.
年份序号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
年养殖山羊y/万只 | 1.2 | 1.5 | 1.6 | 1.6 | 1.8 | 2.5 | 25 | 2.6 | 2.7 |
根据表中的数据和所给统计量,求![]() 关于
关于![]() 的线性回归方程(参考统计量:
的线性回归方程(参考统计量:![]() ,
,![]() );
);
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为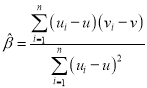 ,
,![]() .
.
【题目】某公司培训员工某项技能,培训有如下两种方式:
方式一:周一到周五每天培训1小时,周日测试
方式二:周六一天培训4小时,周日测试
公司有多个班组,每个班组60人,现任选两组![]() 记为甲组、乙组
记为甲组、乙组![]() 先培训;甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如表:
先培训;甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如表:
第一周 | 第二周 | 第三周 | 第四周 | |
甲组 | 20 | 25 | 10 | 5 |
乙组 | 8 | 16 | 20 | 16 |
![]() 用方式一与方式二进行培训,分别估计员工受训的平均时间
用方式一与方式二进行培训,分别估计员工受训的平均时间![]() 精确到
精确到![]() ,并据此判断哪种培训方式效率更高?
,并据此判断哪种培训方式效率更高?
![]() 在甲乙两组中,从第三周培训后达标的员工中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求这2人中至少有1人来自甲组的概率.
在甲乙两组中,从第三周培训后达标的员工中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求这2人中至少有1人来自甲组的概率.