题目内容
11.已知直线l:y=mx+n.(1)设集合M={-2,-1,1,2,3}和N={-2,3},分别从集合M和N中随机取一个数作为m和n,求直线y=mx+n倾斜角是锐角的概率;
(2)若点(m,n)在由直线x=1,x=-1,y=1,y=-1,x+y-1=0所围成的区域(包括边界)内,求直线y=mx+n的图象不过第四象限的概率.
分析 (1)根据古典概率的概率公式求出基本事件的个数即可求出概率.
(2)根据集合概型的概率的公式即可求出对应的概率
解答 解:(1)抽取的全部结果的基本事件有:(-2,-2),(-2,3),(-1,-2),(-1,3),(1,-2),(1,3),(2,-2),(2,3),(3,-2),(3,3),共10个基本事件,
设“使直线l倾斜角是锐角”的事件为A,则A包含的基本事件有:(1,-2),(1,3),(2,-2),(2,3),(3,-2),(3,3),共6个基本事件,
所以,P(A)=$\frac{6}{10}$=$\frac{3}{5}$.
(2)点(m、n)在由直线x=1,x=-1,y=1,y=-1,x+y-1=0所围成的区域(包括边界)内,满足条件时的区域如图所示:面积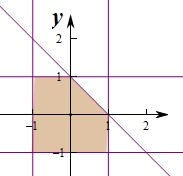 为2×2-$\frac{1}{2}$=$\frac{7}{2}$,
为2×2-$\frac{1}{2}$=$\frac{7}{2}$,
要使直线不过第四象限,则m≥0,n≥0,故满足条件的区域为第一象限的阴影部分,面积为$\frac{1}{2}$,
∴所求事件的概率为P=$\frac{\frac{1}{2}}{\frac{7}{2}}=\frac{1}{7}$.
点评 本题主要考查古典概型和几何概型的概率求法,要求熟练掌握相应的概率公式,特别是几何概型的概率求法,要注意事件的测度;考查学生的计算能力.

练习册系列答案
相关题目
2.等差数列{an}中,a1>0,d<0,S3=S11,则Sn中的最大值是( )
| A. | S7 | B. | S7或S8 | C. | S14 | D. | S8 |
6.不等式x2-2x+1≥a2-2a对任意实数x恒成立,则实数a的取值范围为( )
| A. | (-∞,0]∪[2,+∞) | B. | (-∞,-2]∪[0,+∞) | C. | [0,2] | D. | [-2,0] |
1.设随机变量ξ服从正态分布N(2,9),若p(ξ>c+5)=P(ξ<c-1),则c=( )
| A. | 0 | B. | 2 | C. | 3 | D. | 4 |