题目内容
19.已知曲线C的极坐标方程为4ρ2cos2θ+9ρ2sin2θ=36,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系;(Ⅰ)求曲线C的直角坐标方程;
(Ⅱ)若P(x,y)是曲线C上的一个动点,求3x+4y的最大值.
分析 (I)利用$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$即可得出;
(II)设P(3cosθ,2sinθ),代入3x+4y=$\sqrt{145}$sin(θ+φ),利用三角函数的单调性即可得出.
解答 解:(Ⅰ)由4ρ2cos2θ+9ρ2sin2θ=36得4x2+9y2=36,
化为$\frac{x^2}{9}+\frac{y^2}{4}=1$;
(Ⅱ)设P(3cosθ,2sinθ),
则3x+4y=$9cosθ+8sinθ=\sqrt{145}sin(θ+φ)$,
∵θ∈R,∴当sin(θ+φ)=1时,3x+4y的最大值为$\sqrt{145}$.
点评 本题考查了椭圆的极坐标方程、三角函数的单调性与值域,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
9.若(2x-3)3=a0+a1x+a2x2+a3x3,则(a0+a2)2-(a1+a3)2的值为( )
| A. | -125 | B. | 0 | C. | 2 | D. | 125 |
14.已知直线l过点(1,0)和点($0,\sqrt{3}$),则直线l的倾斜角的大小是( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
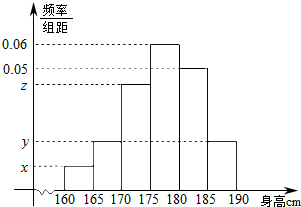 从某学校的800名男生中抽 取40名测量身高,并制成如下频率分布直方图,已知x:y:z=1:2:4.
从某学校的800名男生中抽 取40名测量身高,并制成如下频率分布直方图,已知x:y:z=1:2:4.