题目内容
20.椭圆x216+y24=1x216+y24=1的焦点为F1,F2,点P为其上的动点,当∠F1PF2为钝角时,求P点的横坐标的取值范围.分析 利用余弦定理可知cos∠F1PF2=|PF1|2+|PF2|2−|F1F2|22|PF1|•|PF2||PF1|2+|PF2|2−|F1F2|22|PF1|∙|PF2|<0,通过设P(x0,y0),利用y02y02=16−x02416−x024,代入计算即得结论.
解答 解:由题可知:F1(-2√32√3,0),F2(2√32√3,0),
∵∠F1PF2为钝角,
∴cos∠F1PF2=|PF1|2+|PF2|2−|F1F2|22|PF1|•|PF2||PF1|2+|PF2|2−|F1F2|22|PF1|∙|PF2|<0,
设P(x0,y0),则(x0+2√3)2+y02+(x0−2√3)2+y02−(4√3)22√(x0+2√3)2+y02•√(x0−2√3)2+y02<0,
∴(x0+2√3)2+y02+(x0−2√3)2+y02-(4√3)2<0,
又∵y02=16−x024,
∴(x0+2√3)2+(x0−2√3)2+2•16−x024-(4√3)2<0,
解得:-43√6<x0<43√6.
点评 本题考查椭圆的简单性质,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
12.已知随机变量ξ+η=8,若ξ~B(10,0.4),则E(η),D(η)分别是( )
| A. | 4和2.4 | B. | 2和2.4 | C. | 6和2.4 | D. | 4和5.6 |
10.等比数列{an}中,首项a1=2015,公比q=-12,记Tn为它的前n项之积,则Tn最大时,n的值为( )
| A. | 9 | B. | 11 | C. | 12 | D. | 13 |
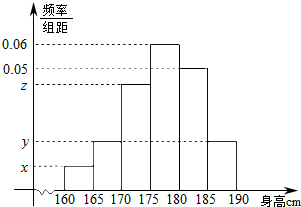 从某学校的800名男生中抽 取40名测量身高,并制成如下频率分布直方图,已知x:y:z=1:2:4.
从某学校的800名男生中抽 取40名测量身高,并制成如下频率分布直方图,已知x:y:z=1:2:4.