Question

【题目】如图，长方体ABCD﹣A1B1C1D1中，AB＝BC＝4，BB1＝2，点E、F、M分别为C1D1，A1D1，B1C1的中点，过点M的平面α与平面DEF平行，且与长方体的面相交，交线围成一个几何图形．

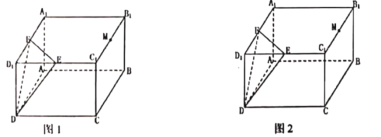
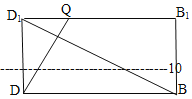
（1）在图1中，画出这个几何图形，并求这个几何图形的面积（不必说明画法与理由）

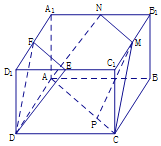
（2）在图2中，求证：D1B⊥平面DEF．

Answer 1

【答案】（1）6（2）见解析

【解析】

（1）取A1 B1中点为N,连接N与M，则几何图形为ACMN,再求其面积。

（2）建系，利用向量的数量积等于0,说明两直线垂直。

（1）设N为A1B1的中点，连结MN，AN、AC、CM，

则四边形MNAC为所作图形．

由题意知MN∥A1C1（或∥EF），四边形MNAC为梯形，

且MNAC＝2，

过M作MP⊥AC于点P，

可得MC2，PC，

得MP，

∴梯形MNAC的面积（24）6．

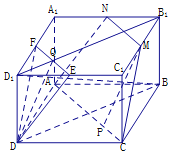
证明：（2）示例一：在长方体中ABCD﹣A1B1C1D1，

设D1B1交EF于Q，连接DQ，

则Q为EF的中点并且为D1B1的四等点，如图，

D1Q4，

由DE＝DF得DQ⊥EF，又EF⊥BB1，

∴EF⊥平面BB1D1D，∴EF⊥D1B，

，∴∠D1QD＝∠BD1D，

∴∠QD1B+∠D1QD＝∠DD1B+∠BD1Q＝90°，

∴DQ⊥D1B，∴D1B⊥平面DEF．

示例二：设D1B1交EF于Q，连接DQ，则Q为EF的中点，

且为D1B1的四等分点，D1Q4，

由BB1⊥平面A1B1C1D1可知BB1⊥EF，

又B1D1⊥EF，BB1∩B1D1＝B1，∴EF⊥平面BB1D1D，∴EF⊥D1B，

由，得tan∠QDD1＝tan∠D1BD，

得∠QDD1＝∠D1BD，∴∠QDB+∠D1BD＝∠QDB+∠QDD1＝90°，

∴DQ⊥D1B，又DQ∩EF＝Q，∴D1B⊥平面DEF．

；