题目内容
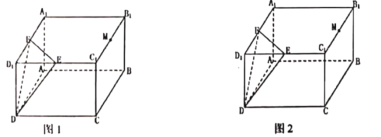
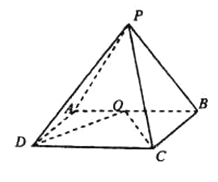
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,底面
,底面![]() 为矩形,
为矩形,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() .
.
(1)求证:![]() ;
;
(2)若![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明详见解析;(2)![]() .
.
【解析】
试题分析:本题主要考查线面垂直的判定、二面角的求解等基础知识,考查学生的分析问题解决问题的能力、空间想象能力和逻辑推理能力.第一问,利用面面垂直的性质先得到线面垂直![]()
![]() 平面
平面![]() ,从而得到线线垂直
,从而得到线线垂直![]() ,利用线面垂直的判定得
,利用线面垂直的判定得![]() 平面
平面![]() ,最后利用性质定理得到
,最后利用性质定理得到![]() ;第二问,法一:利用线面及三角形相似等知识判断出
;第二问,法一:利用线面及三角形相似等知识判断出![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角,再在三角形中利用余弦定理解题;法二:利用向量法先建立空间直角坐标系,利用夹角公式计算二面角的余弦值.
所成的角,再在三角形中利用余弦定理解题;法二:利用向量法先建立空间直角坐标系,利用夹角公式计算二面角的余弦值.
试题解析:(Ⅰ)证明:连结![]() ,因
,因![]() ,
,![]() 为
为![]() 的中点
的中点
故![]() .
.
∵侧面![]()
![]() 底面
底面![]()
∴![]()
![]() 平面
平面![]()
∴![]() ,
,![]()
∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴![]() ,
,
又∵![]() ,故
,故![]()
![]() 平面
平面![]()
所以![]() .
.
(Ⅱ)解法一:在矩形![]() 中,由(Ⅰ)得
中,由(Ⅰ)得![]() ,所以
,所以![]() ,不妨设
,不妨设![]() 则
则![]() .
.
∵侧面![]()
![]() 底面
底面![]() ,底面
,底面![]() 为矩形
为矩形
∴![]() 平面
平面![]()
![]() 平面
平面![]()
![]() ≌
≌![]()
∴![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角
所成的角
∴![]() =
=![]() ,
,![]() =
=![]() ,
,![]()
∴![]() ,∴
,∴![]() 为等边三角形,
为等边三角形,
设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,则
,则![]()
在![]() 中,过
中,过![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,则
,则![]() 为二面角
为二面角![]() 的一个平面角。
的一个平面角。
由于![]() =
=![]() ,
,![]() ,所以在
,所以在![]() 中,
中,![]() ,
,![]()
∵![]()
∴![]()
∴![]()
∴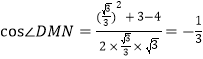
即二面角![]() 的余弦值
的余弦值![]() .
.
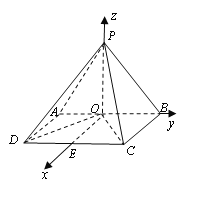
解法二:取![]() 的中点
的中点![]() ,以
,以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 所在的直线分别为
所在的直线分别为![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() .不妨设
.不妨设![]() ,则
,则![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,
,![]() ,从而
,从而![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
由 ,得,
,得,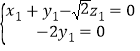
可取![]() .
.
同理,可取平面![]() 的一个法向量为
的一个法向量为![]() .
.
于是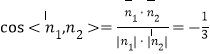 ,
,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某小组为了研究昼夜温差对一种稻谷种子发芽情况的影响,他们分别记录了4月1日至4月5日的每天星夜温差与实验室每天每100颗种子的发芽数,得到如下资料:
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 |
温差 | 9 | 10 | 11 | 8 | 12 |
发芽数 | 38 | 30 | 24 | 41 | 17 |
利用散点图,可知![]() 线性相关。
线性相关。
(1)求出![]() 关于
关于![]() 的线性回归方程,若4月6日星夜温差
的线性回归方程,若4月6日星夜温差![]() ,请根据你求得的线性同归方程预测4月6日这一天实验室每100颗种子中发芽颗数;
,请根据你求得的线性同归方程预测4月6日这一天实验室每100颗种子中发芽颗数;
(2)若从4月1日![]() 4月5日的五组实验数据中选取2组数据,求这两组恰好是不相邻两天数据的概率.
4月5日的五组实验数据中选取2组数据,求这两组恰好是不相邻两天数据的概率.
(公式: )
)
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨)标准煤的几组对照数据
(吨)标准煤的几组对照数据
|
|
|
|
|
|
|
|
|
|
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
参考公式: