题目内容
已知椭圆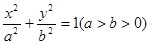 的左右焦点分别为
的左右焦点分别为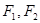 ,短轴两个端点为
,短轴两个端点为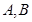 ,且四边形
,且四边形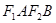 是边长为2的正方形.
是边长为2的正方形.
(1)求椭圆的方程;
(2)若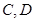 分别是椭圆长轴的左右端点,动点
分别是椭圆长轴的左右端点,动点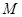 满足
满足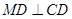 ,连接
,连接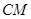 ,交椭圆于点
,交椭圆于点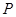 .证明:
.证明: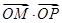 为定值;
为定值;
(3)在(2)的条件下,试问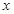 轴上是否存在异于点
轴上是否存在异于点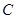 的定点
的定点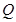 ,使得以
,使得以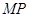 为直径的圆恒过直线
为直径的圆恒过直线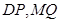 的交点,若存在,求出点
的交点,若存在,求出点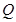 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(1)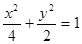 ;(2)证明见解析;(3)存在,
;(2)证明见解析;(3)存在,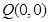 .
.
解析试题分析:(1)由椭圆的几何性质知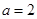 ,
,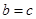 ,结合
,结合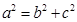 可很快求得
可很快求得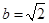 ,这样就得出了椭圆的标准方程;(2)若
,这样就得出了椭圆的标准方程;(2)若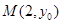 ,
,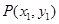 ,则
,则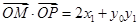 ,因此我们要把
,因此我们要把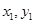 用
用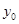 表示出来,先用
表示出来,先用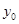 把直线
把直线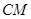 方程写出,然后与椭圆方程联立解方程组可得
方程写出,然后与椭圆方程联立解方程组可得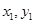 (注意消去
(注意消去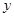 得关于
得关于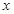 的二次方程,这个二次方程有一个解是
的二次方程,这个二次方程有一个解是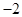 ,另一解是
,另一解是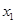 ,这样很容易得到
,这样很容易得到 ,于是有
,于是有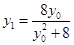 );(3)这是存在性命题,总是假设
);(3)这是存在性命题,总是假设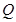 点存在,设
点存在,设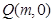 ,由题意则应该有
,由题意则应该有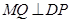 ,即
,即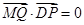 ,而点
,而点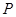 的坐标在(2)中已经用
的坐标在(2)中已经用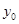 表示出来了,因此利用
表示出来了,因此利用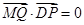 若能求出
若能求出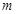 ,则说明符合题意的点
,则说明符合题意的点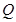 存在,否则就不存在.
存在,否则就不存在.
(1)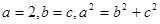 ,
, ,
,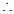 椭圆方程为
椭圆方程为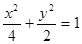 4分
4分
(2) ,设
,设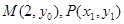 ,则
,则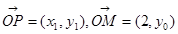 .
.
直线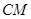 :
: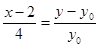 ,即
,即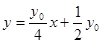 ,
,
代入椭圆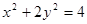 得
得 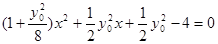
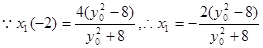 ,
,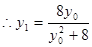 .
. 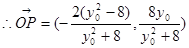 ,
, 
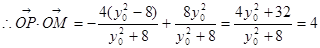 (定值). 10分
(定值). 10分
(3)设存在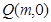 满足条件,则
满足条件,则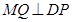 .
. 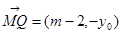 ,
,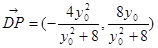 ,
,
则由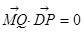 得
得 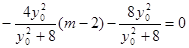 ,从而得
,从而得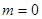 .
. 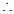 存在
存在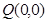 满足条件 16分
满足条件 16分
考点:(1)椭圆标准方程;(2)解析几何中的定值问题;(3)解析几何中的存在性命题.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
 (a∈R).
(a∈R).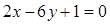 并且与曲线
并且与曲线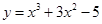 相切的直线方程.
相切的直线方程. :
: 内有一点
内有一点 ,过点
,过点 作直线
作直线 交圆
交圆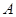 ,
, 两点.
两点. 被点
被点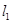 :
: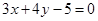 与直线
与直线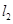 :
: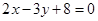 的交点
的交点 ,且满足下列条件的直线方程
,且满足下列条件的直线方程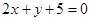 平行 ;
平行 ;  ,过左焦点F1作x轴的垂线交椭圆于A、A′两点,|AA′|=4.
,过左焦点F1作x轴的垂线交椭圆于A、A′两点,|AA′|=4.
