题目内容
求垂直于直线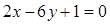 并且与曲线
并且与曲线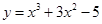 相切的直线方程.
相切的直线方程.
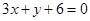 .
.
解析试题分析:先根据所求直线与直线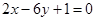 垂直求出所求直线的斜率
垂直求出所求直线的斜率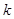 ,然后设出切点
,然后设出切点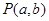 ,由
,由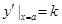 ,计算出
,计算出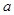 的值,接着计算出
的值,接着计算出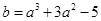 的值,最后可写出切线的方程:
的值,最后可写出切线的方程: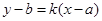 ,并化成一般方程即可.
,并化成一般方程即可.
试题解析:因为直线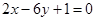 的斜率为
的斜率为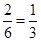 ,所以垂直于直线
,所以垂直于直线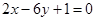 并且与曲线
并且与曲线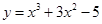 相切的直线的斜率为
相切的直线的斜率为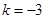
设切点为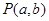 ,函数
,函数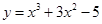 的导数为
的导数为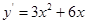
所以切线的斜率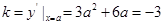 ,得
,得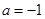
代入到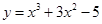 得
得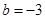 ,即
,即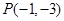
∴所求切线的方程为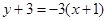 即
即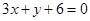 .
.
考点:1.两直线垂直的判定与性质;2.导数的几何意义.

练习册系列答案
相关题目
设椭圆C1和抛物线C2的焦点均在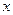 轴上,C1的中心和C2的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表中:
轴上,C1的中心和C2的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表中:
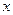 | 3 | -2 | 4 | 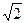 |
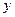 | 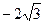 | 0 | -4 | 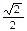 |
(1)求曲线C1,C2的标准方程;
(2)设直线
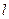 与椭圆C1交于不同两点M、N,且
与椭圆C1交于不同两点M、N,且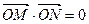 。请问是否存在直线
。请问是否存在直线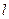 过抛物线C2的焦点F?若存在,求出直线
过抛物线C2的焦点F?若存在,求出直线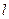 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.  ,第二次掷出的点数为
,第二次掷出的点数为 .试就方程组
.试就方程组 (※)解答下列问题:
(※)解答下列问题: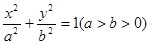 的左右焦点分别为
的左右焦点分别为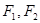 ,短轴两个端点为
,短轴两个端点为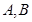 ,且四边形
,且四边形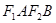 是边长为2的正方形.
是边长为2的正方形.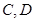 分别是椭圆长轴的左右端点,动点
分别是椭圆长轴的左右端点,动点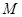 满足
满足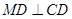 ,连接
,连接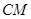 ,交椭圆于点
,交椭圆于点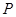 .证明:
.证明: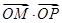 为定值;
为定值;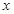 轴上是否存在异于点
轴上是否存在异于点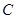 的定点
的定点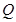 ,使得以
,使得以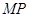 为直径的圆恒过直线
为直径的圆恒过直线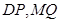 的交点,若存在,求出点
的交点,若存在,求出点
 中,顶点
中,顶点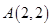 ,边
,边 上的中线
上的中线 所在直线的方程是
所在直线的方程是 ,边
,边 上高
上高 所在直线的方程是
所在直线的方程是 .
. 、C的坐标; (2)求
、C的坐标; (2)求 ,直线
,直线 经过定点,定点坐标为 ▲
经过定点,定点坐标为 ▲