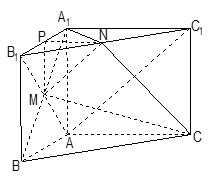
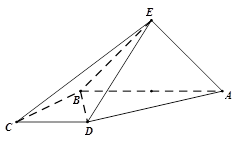
题目内容
如图, 中,侧棱与底面垂直,
中,侧棱与底面垂直, ,
, ,点
,点 分别为
分别为 和
和 的中点.
的中点.

(1)证明: ;
;
(2)求二面角 的正弦值.
的正弦值.
 中,侧棱与底面垂直,
中,侧棱与底面垂直, ,
, ,点
,点 分别为
分别为 和
和 的中点.
的中点.
(1)证明:
 ;
;(2)求二面角
 的正弦值.
的正弦值.(1)利用线线平行证明线面平行;(2)利用定义法或向量法求二面角
试题分析:
(1)证法一: 连接
 1分
1分由题意知,点
 分别为
分别为 和
和 的中点,
的中点, . 3分
. 3分又
 平面
平面 ,
, 平面
平面 , 5分
, 5分 平面
平面 . 6分
. 6分证法二:取
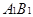 中点
中点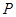 ,连
,连 ,而
,而 分别为
分别为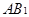 与
与 的中点,
的中点,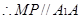 , 2分
, 2分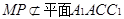 ,
,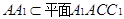 ,
,  ,
, 同理可证
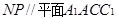 4分
4分又
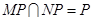
 平面
平面 //平面
//平面 . 5分
. 5分 平面
平面 ,
, 平面
平面 . 6分
. 6分证法三(向量法):以点
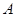 为坐标原点,分别以直线
为坐标原点,分别以直线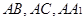 为
为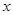 轴,
轴, 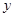 轴,
轴, 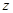 轴建立空间直角坐标系
轴建立空间直角坐标系 ,如图所示.
,如图所示.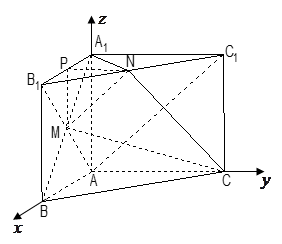
于是
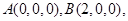
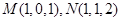
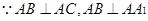 ,
,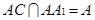 ,
,
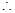 向量
向量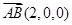 是 平面
是 平面 的一个法向量 2分
的一个法向量 2分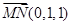 ,
,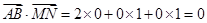
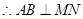 4分
4分又
 5分
5分 平面
平面 . 6分
. 6分(2)解法一: 以点
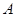 为坐标原点,分别以直线
为坐标原点,分别以直线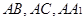 为
为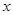 轴,
轴, 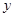 轴,
轴, 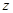 轴建立空间直角坐标系
轴建立空间直角坐标系 ,如图所示.
,如图所示.于是
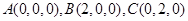 ,
,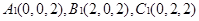 ,
,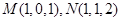 8分
8分由(1)知
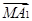 是平面
是平面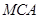 的一个法向量,
的一个法向量, 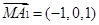 . 10分
. 10分设平面
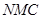 的法向量为
的法向量为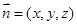 ,
,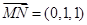 ,
, ,
,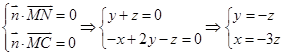 ,
,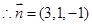 12分
12分设向量
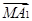 和向量
和向量 的夹 角为
的夹 角为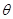 ,则
,则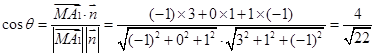 13分
13分 二面角
二面角 的的正弦值为
的的正弦值为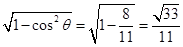 14分
14分解法二(几何法):如图,将几何体补形成一 个正方体,连
 交于点
交于点 ,连
,连 ,
,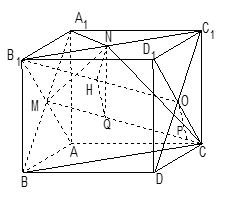
显然,
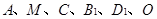 ,都在同一平面
,都在同一平面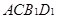 上.…………7分
上.…………7分易证
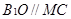 ,
,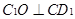 ,
,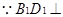 平面
平面 ,
, 平面
平面 ,
, ,又
,又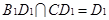
 平面
平面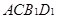 .
.取
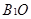 中点
中点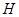 ,连
,连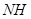 ,
,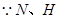 分别是
分别是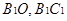 的中点
的中点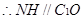 ,
,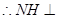 平面
平面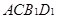 , …………9分
, …………9分且
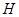 为垂足,即
为垂足,即 平 面
平 面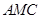 ,过点
,过点 作
作 于
于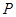 ,
,过
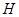 作
作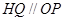 交
交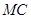 于
于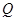 ,连
,连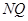 ,
,则
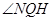 即是所求二面角
即是所求二面角 的补角. …………11分
的补角. …………11分在
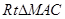 中,
中,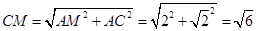 ,
,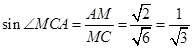 ,
,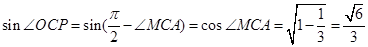 ,
,在
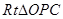 中,
中,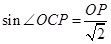 ,
,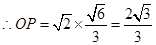
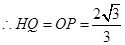 又
又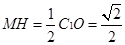
 在
在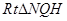 中,
中,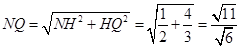 , …………12分
, …………12分 . …………13分
. …………13分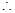 所求二面角
所求二面角 的正弦值为
的正弦值为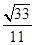 …………14分
…………14分点评:高考中对立体几何解答题的考查一般都体现为一题两法(同一题两种解法:传统法与向量法).而运用向量在解决立体几何问题主要集中在法向量的应用上,它可以证明空间线面的位置关系、求解空间角、距离.同时运用空间向量解答立体几何问题,淡化了传统立体几何中的“形”的推理方法,强化了代数运算,从而降低了思维难度,且思路明确,过程较为程序化.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
 中,
中, ,
, ,
, 为
为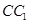 的中点,则异面直线
的中点,则异面直线 与
与 所成角的余弦值为
所成角的余弦值为



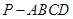 中,侧棱都相等,底面是边长为
中,侧棱都相等,底面是边长为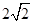 的正方形,底面中心为
的正方形,底面中心为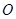 ,以
,以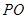 为直径的球经过侧棱中点,则该球的体积为( )
为直径的球经过侧棱中点,则该球的体积为( )
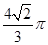


 ,
, ∥
∥ ,
, .又
.又 ,
, ,直线AM与直线PC所成的角为
,直线AM与直线PC所成的角为 .
.
 ;
; 的余弦值.
的余弦值.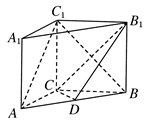
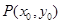
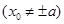 是双曲线
是双曲线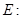
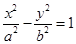
 上一点,
上一点, 、
、 分别是双曲线
分别是双曲线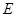 的左、右顶点,直线
的左、右顶点,直线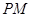 ,
,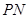 的斜率之积为
的斜率之积为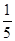 .
.
 ,
, 两点,
两点, 为坐标原点,
为坐标原点,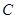 为双曲线上一点,满足
为双曲线上一点,满足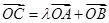 ,求
,求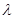 的值.
的值. 与
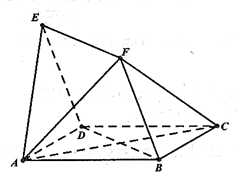
与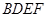 均为菱形,
均为菱形,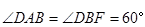 ,且
,且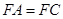 .
.
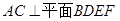 ;
;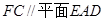 ;
;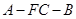 的余弦值.
的余弦值.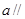 平面
平面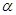 ,则
,则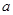 平行;
平行;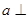 平面
平面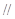 平面
平面 ,则
,则 平面
平面