题目内容
正方体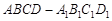 中,M、N分别是棱CD1、CC1的中点,则异面直线MA1与DN所成角的余弦值是 .
中,M、N分别是棱CD1、CC1的中点,则异面直线MA1与DN所成角的余弦值是 .
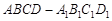 中,M、N分别是棱CD1、CC1的中点,则异面直线MA1与DN所成角的余弦值是 .
中,M、N分别是棱CD1、CC1的中点,则异面直线MA1与DN所成角的余弦值是 .0
试题分析:以D为坐标原点,建立空间直角坐标系
 ,利用向量的方法求出
,利用向量的方法求出 与
与 夹角求出异面直线A1M与DN所成的角.解:以D为坐标原点,建立如图所示的空间直角坐标系.设棱长为2,
夹角求出异面直线A1M与DN所成的角.解:以D为坐标原点,建立如图所示的空间直角坐标系.设棱长为2,则D(0,0,0),N(0,2,1),M(0,1,0),A1(2,0,2),
 =(0,2,1),
=(0,2,1), =(﹣2,1,﹣2),
=(﹣2,1,﹣2), •
• =0,所以
=0,所以 ⊥
⊥ ,即A1M⊥DN,异面直线A1M与DN所成的角的大小是90°,故答案为:0
,即A1M⊥DN,异面直线A1M与DN所成的角的大小是90°,故答案为:0点评:本题考查空间异面直线的夹角求解,采用了向量的方法.向量的方法能降低空间想象难度,但要注意有关点,向量坐标的准确.否则容易由于计算失误而出错

练习册系列答案
相关题目
 中,
中, ,
, ,
, 为
为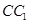 的中点,则异面直线
的中点,则异面直线 与
与 所成角的余弦值为
所成角的余弦值为



 中
中 ,
, 面
面 ,
, ,
, 面
面 .
.
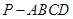 中,侧棱都相等,底面是边长为
中,侧棱都相等,底面是边长为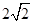 的正方形,底面中心为
的正方形,底面中心为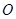 ,以
,以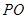 为直径的球经过侧棱中点,则该球的体积为( )
为直径的球经过侧棱中点,则该球的体积为( )
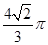


 平面
平面 ,
, ,
, ,
, ,
, 分别为
分别为 的中点.
的中点.
 平面
平面 ;
; 与平面
与平面 所成角的正弦值.
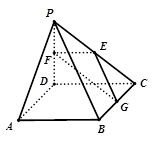
所成角的正弦值.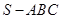 中,侧面
中,侧面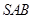 与侧面
与侧面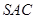 均为等边三角形,
均为等边三角形, 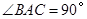 ,
,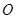 为
为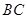 中点.
中点.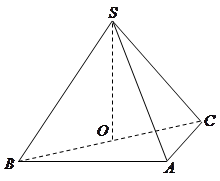
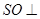 平面
平面 ;
;
 ,
, ∥
∥ ,
, .又
.又 ,
, ,直线AM与直线PC所成的角为
,直线AM与直线PC所成的角为 .
.
 ;
; 的余弦值.
的余弦值. 与
与 均为菱形,
均为菱形,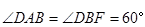 ,且
,且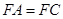 .
.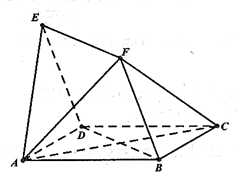
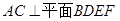 ;
;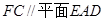 ;
;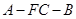 的余弦值.
的余弦值.