Question

【题目】已知椭圆C： （a＞b＞0）的两个焦点F1 ， F2和上下两个顶点B1 ， B2是一个边长为2且∠F1B1F2为60°的菱形的四个顶点．
（1）求椭圆C的方程；
（2）过右焦点F2 ， 斜率为k（k≠0）的直线与椭圆C相交于E，F两点，A为椭圆的右顶点，直线AE，AF分别交直线x=3于点M，N，线段MN的中点为P，记直线PF2的斜率为k′．求证：kk′为定值．

Answer 1

【答案】
（1）解：由题意可得a=2， ，c=1．

∴椭圆C的方程为

（2）解：设过点F2（1，0）的直线l的方程为：y=k（x﹣1）．

设点E（x1，y1），F（x2，y2），联立 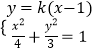，化为（3+4k2）x2﹣8k2x+4k2﹣12=0．

显然△＞0，∴ ， （*）．

直线AE的方程为 ，直线AF的方程为 ，

令x=3，得点M ，N ．

∴点P ．

直线PF2的斜率为k′=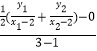

=

=

= ．

把（*）代入得k′= =﹣ ．

∴ 为定值

【解析】解：（1）由题意利用菱形和含30°角的直角三角形的性质可得a=2， ，c=1．即可得到椭圆C的方程．（2）设过点F2（1，0）的直线l的方程为：y=k（x﹣1）．设点E（x1 ， y1），F（x2 ， y2），与椭圆方程联立即可得到根与系数的关系，．可得直线AE的方程及直线AF的方程，令x=3，得点M，N的坐标．利用中点坐标公式可得点P的坐标．即可得到直线PF2的斜率为k′，把根与系数代入即可得出kk′为定值．