题目内容
【题目】已知函数f(x)=(ax2+x﹣1)ex , 其中e是自然对数的底数,a∈R.
(Ⅰ)若a=1.求曲线f(x)在点(1,f(1))处的切线方程;
(Ⅱ)若a=﹣1,函数f(x)的图象与函数g(x)=![]() x3+
x3+![]() x2+m的图象有3个不同的交点,求实数m的取值范围.
x2+m的图象有3个不同的交点,求实数m的取值范围.
【答案】解:(Ⅰ)∵f(x)=(x2+x﹣1)ex ,
∴f′(x)=(2x+1)ex+(x2+x﹣1)ex=(x2+3x)ex .
∴曲线f(x)在点(1,f(1))处的切线斜率k=f′(1)=4e,
∵f(1)=e,
∴曲线f(x)在点(1,f(1))处的切线方程为y﹣e=4e(x﹣1),
即4ex﹣y﹣3e=0.
(Ⅱ)令h(x)=f(x)﹣g(x)=(﹣x2+x﹣1)ex﹣(![]() x3+
x3+![]() x2+m)
x2+m)
则h′(x)=(﹣2x+1)ex+(﹣x2+x﹣1)ex﹣(x2+x)
=﹣(ex+1)(x2+x)
令h′(x)>0得﹣1<x<0,令h′(x)<0得x>0或x<﹣1.
∴h(x)在x=﹣1处取得极小值h(﹣1)=﹣![]() ﹣
﹣![]() ﹣m,在x=0处取得极大值h(0)=﹣1﹣m,
﹣m,在x=0处取得极大值h(0)=﹣1﹣m,
∵函数f(x),g(x)的图象有三个交点,即函数h(x)有3个不同的零点,
∴![]() 即
即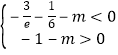 ,
,
解得:﹣![]() ﹣
﹣![]() <m<﹣1.
<m<﹣1.
【解析】(Ⅰ)求出导数,求出切线的斜率,切点,运用点斜式方程,即可得到;
(Ⅱ)令h(x)=f(x)﹣g(x),求出导数,求出单调区间,和极值,函数f(x),g(x)的图象有三个交点,即函数h(x)有3个不同的零点,即有h(﹣1)<0,且h(0)>0,解出即可.

【题目】某地区2007年至2013年农村居民家庭纯收入![]() (单位:千元)的数据如下表:
(单位:千元)的数据如下表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入 | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于![]() 的线性回归方程;
的线性回归方程;
(2)判断y与![]() 之间是正相关还是负相关?
之间是正相关还是负相关?
(3)预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为: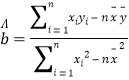 ,
,![]()
【题目】在某学校进行的一次语文与历史成绩中,随机抽取了25位考生的成绩进行分析,25位考生的语文成绩已经统计在茎叶图中,历史成绩如下:
(Ⅰ)请根据数据在茎叶图中完成历史成绩统计;
(Ⅱ)请根据数据完成语文成绩的频数分布表及语文成绩的频率分布直方图;
语文成绩的频数分布表:
语文成绩分组 | [50,60) | [60,70) | [70,80) | [90,100) | [100,110) | [110,120] |
频数 |