题目内容
【题目】(1)求与椭圆![]() 有公共焦点,并且离心率为
有公共焦点,并且离心率为![]() 的双曲线方程.
的双曲线方程.
(2)已知斜率为1的直线l过椭圆![]() 的右焦点F交椭圆于A、B两点,求弦AB的长.
的右焦点F交椭圆于A、B两点,求弦AB的长.
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
(1)根据题意,求出椭圆![]() 的焦点坐标,分析可得要求双曲线的焦点在x轴上,且c=
的焦点坐标,分析可得要求双曲线的焦点在x轴上,且c=![]() ,设其方程为
,设其方程为![]() ﹣
﹣![]() =1,由离心率公式求出a的值,由双曲线的几何性质计算可得b的值,将a、b的值代入双曲线方程即可得答案;(2)设出A、B的坐标,由椭圆方程求出椭圆右焦点坐标,得到A、B所在直线方程,与椭圆方程联立,化为关于x的一元二次方程,利用根与系数的关系可得A、B横坐标的和与积,代入弦长公式求弦AB的长.
=1,由离心率公式求出a的值,由双曲线的几何性质计算可得b的值,将a、b的值代入双曲线方程即可得答案;(2)设出A、B的坐标,由椭圆方程求出椭圆右焦点坐标,得到A、B所在直线方程,与椭圆方程联立,化为关于x的一元二次方程,利用根与系数的关系可得A、B横坐标的和与积,代入弦长公式求弦AB的长.
(1)由椭圆方程为![]() ,知长半轴长
,知长半轴长![]() ,短半轴长
,短半轴长![]() ,
,
焦距的一半![]() ,
,
∴焦点是![]() ,
,![]() ,因此双曲线的焦点也是
,因此双曲线的焦点也是![]() ,
,![]() ,
,
设双曲线方程为![]() ,由题设条件及双曲线的性质,得
,由题设条件及双曲线的性质,得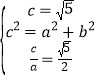 ,解得
,解得![]() ,故所求双曲线的方程为
,故所求双曲线的方程为![]() .
.
(2)设A、B的坐标分别为![]() 、
、![]() .
.
由椭圆的方程知![]() ,
,![]() ,
,![]() ,∴
,∴![]() .
.
直线l的方程为![]() ① 将①代入
① 将①代入![]() ,化简整理得
,化简整理得
![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() .
.

练习册系列答案
相关题目