题目内容
9.如图,平行四边形ABCD中,E是DC的中点,AE交BD于M,试用向量的方法证明,M是BD的一个三等分点.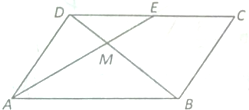
分析 将$\overrightarrow{BM}$两次表示,利用向量分解定理,即可得出结论.
解答 证明:设$\overrightarrow{BM}$=t$\overrightarrow{BD}$,∵$\overrightarrow{BD}$=$\overrightarrow{BA}$+$\overrightarrow{AD}$,∴$\overrightarrow{BM}$=t$\overrightarrow{BA}$+t$\overrightarrow{BC}$.
又∵$\overrightarrow{BM}$=k$\overrightarrow{BA}$+(1-k)$\overrightarrow{BE}$=k$\overrightarrow{BA}$+(1-k)$\overrightarrow{BC}$+$\frac{1}{2}$(1-k)$\overrightarrow{CD}$
=$\frac{1}{2}$(1+k)$\overrightarrow{BA}$+(1-k)$\overrightarrow{BC}$.
由向量分解定理,$\overrightarrow{BM}$的表示是唯一的,
∴t=$\frac{1}{2}$(1+k)且t=1-k,解得:t=$\frac{2}{3}$,即M是BD的一个三等分点.
点评 本题考查向量分解定理,考查学生的计算能力,正确表示向量是关键.

练习册系列答案
相关题目
19.已知直线l:x-y+m=0与椭圆C:$\frac{{x}^{2}}{2}$+y2=1交于不同的两点A,B,且线段AB的中点不在圆x2+y2=$\frac{5}{9}$内,则m的取值范围为( )
| A. | m≥1或m≤-1 | B. | -$\sqrt{3}$≤m≤-1或1≤≤m≤$\sqrt{3}$ | C. | -1≤m≤1 | D. | -$\sqrt{3}$<m≤-1或1≤m<$\sqrt{3}$ |
17.下列命题错误的是( )
| A. | 命题“?x∈R,x2-x+1≥$\frac{3}{4}$”的否定是“?x0∈R,x02-x0+1<$\frac{3}{4}$” | |
| B. | 命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0” | |
| C. | 命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0” | |
| D. | 若命题“非p”与命题“p或q”都是真命题,那么q一定是假命题 |
4.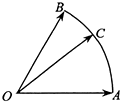 己知C是半径为1、圆心角为60°的圆弧上的动点,如图,若$\overrightarrow{OC}$=x$\overline{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x+y的最大值是( )
己知C是半径为1、圆心角为60°的圆弧上的动点,如图,若$\overrightarrow{OC}$=x$\overline{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x+y的最大值是( )
 己知C是半径为1、圆心角为60°的圆弧上的动点,如图,若$\overrightarrow{OC}$=x$\overline{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x+y的最大值是( )
己知C是半径为1、圆心角为60°的圆弧上的动点,如图,若$\overrightarrow{OC}$=x$\overline{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x+y的最大值是( )| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{4}{3}$ | C. | 2 | D. | $\frac{\sqrt{3}}{2}$ |
14.已知有序数对(a,b)∈{(a,b)|a∈[0,4],b∈[0,4]},则方程x2-2ax+b=0有实根的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
1.一几何体的三视图如图所示,则它的体积为( )
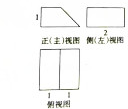

| A. | 2 | B. | 3 | C. | 6 | D. | 9 |
19.设S是整数集Z的非空子集,如果?a,b∈Z,都有a2-b2∈S,则称S是一个好集,已知S是一个“好集”,下面命题为假命题的是( )
| A. | 一切奇数都属于S | B. | 偶数4k-2(k∈Z)都不属于S | ||
| C. | 若x,y∈S,则xy∈S | D. | 若x,y属于S,则x+y∈S |
