题目内容
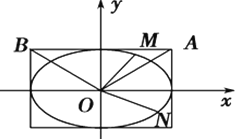
【题目】已知两点
，
，若直线
上存在四个点
，使得
是直角三角形，则实数
的取值范围是（ ）
A.
B.
C.
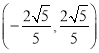D.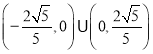
【答案】D
【解析】
根据△MNP是直角三角形，转化为以MN为直径的圆和直线y=k（x-3）相交，且k≠0，然后利用直线和圆相交的等价条件进行求解即可．
当P1M⊥x，P4M⊥x时，此时存在两个直角三角形，
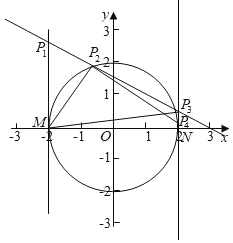
当MN为直角三角形的斜边时，△MNP是直角三角形，
要使直线y=k（x-3）上存在四个点P（i=1，2，3，4），
使得△MNP是直角三角形，等价为以MN为直径的圆和直线y=k（x-3）相交，且k≠0，
圆心O到直线kx-y-3k=0的距离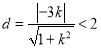
，
平方得9k2<4（1+k2）=4+4k2，
即5k2<4，即k2<
，得
，
又k≠0，∴实数k的取值范围是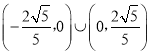
，
故选：D．
练习册系列答案
相关题目
【题目】为了改善空气质量，某市规定，从2018年1月1日起，对二氧化碳排放量超过
的轻型汽车进行惩罚性征税.检测单位对甲乙两品牌轻型汽车各抽取5辆进行二氧化碳排放量检测，记录如下:（单位:
）
甲 | 80 | 110 | 120 | 140 | 150 |
乙 | 100 | 120 |
| 100 | 160 |
经测算得乙品牌轻型汽车二氧化碳排放量的平均值为
.
（1）求表中
的值，并比较甲乙两品牌轻型汽车二氧化碳排放量的稳定性；
（2）从被检测的5辆甲品牌汽车中随机抽取2辆，求至少有1辆二氧化碳排放量超过的概率.（注:方差
，其中
为
的平均数）.
