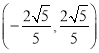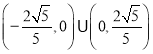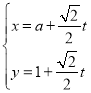题目内容
【题目】已知椭圆![]()
![]() 的长轴长是短轴长的两倍,焦距为
的长轴长是短轴长的两倍,焦距为![]() .
.
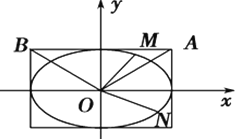
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)不过原点![]() 的直线与椭圆
的直线与椭圆![]() 交于两点
交于两点![]() 、
、![]() ,且直线
,且直线![]() 、
、![]() 、
、![]() 的斜率依次成等比数列,问:直线是否定向的,请说明理由.
的斜率依次成等比数列,问:直线是否定向的,请说明理由.
【答案】(1)![]() ;(2)不定向,理由见解析.
;(2)不定向,理由见解析.
【解析】
(1)由椭圆的长轴长是短轴长的两倍,焦距为![]() ,列出方程组能求出椭圆
,列出方程组能求出椭圆![]() 的标准方程;
的标准方程;
(2)由题意设直线![]() 的方程为
的方程为![]() ,联立直线
,联立直线![]() 与椭圆
与椭圆![]() 的标准方程,由此利用根的判别式、韦达定理、等比数列、椭圆性质,结合已知条件能求出直线
的标准方程,由此利用根的判别式、韦达定理、等比数列、椭圆性质,结合已知条件能求出直线![]() 的方向向量,由此能说明直线
的方向向量,由此能说明直线![]() 不定向.
不定向.
(1)设椭圆![]() 的焦距为
的焦距为![]() ,由已知得
,由已知得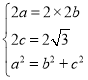 ,解得
,解得![]() ,
,![]() ,
,
![]() 椭圆
椭圆![]() 的标准方程为
的标准方程为![]() ;
;
(2)由题意可设直线的方程为![]() ,
,
联立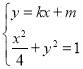 ,消去
,消去![]() 并整理,得
并整理,得![]() ,
,
计算![]() ,此时设
,此时设![]() 、
、![]() ,
,
则![]() ,
,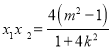 ,
,
于是![]() ,
,
又直线![]() 、
、![]() 、
、![]() 的斜率依次成等比数列,
的斜率依次成等比数列,![]() ,整理得
,整理得![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,![]() ,解得
,解得![]() ,
,
则直线![]() 的方向向量为
的方向向量为![]() ,即直线
,即直线![]() 是不定向的.
是不定向的.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
【题目】某茶楼有四类茶饮,假设为顾客准备泡茶工具所需的时间互相独立,且都是整数分钟,经统计以往为100位顾客准备泡茶工具所需的时间![]() ,结果如下:
,结果如下:
类别 | 铁观音 | 龙井 | 金骏眉 | 大红袍 |
顾客数(人) | 20 | 30 | 40 | 10 |
时间 | 2 | 3 | 4 | 6 |
注:服务员在准备泡茶工具时的间隔时间忽略不计,并将频率视为概率.
(1)求服务员恰好在第6分种开始准备第三位顾客的泡茶工具的概率;
(2)用![]() 表示至第4分钟末已准备好了工具的顾客人数,求
表示至第4分钟末已准备好了工具的顾客人数,求![]() 的分布列及数学期望.
的分布列及数学期望.