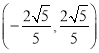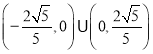题目内容
【题目】为了改善空气质量，某市规定，从2018年1月1日起，对二氧化碳排放量超过
的轻型汽车进行惩罚性征税.检测单位对甲乙两品牌轻型汽车各抽取5辆进行二氧化碳排放量检测，记录如下:（单位:
）
甲 | 80 | 110 | 120 | 140 | 150 |
乙 | 100 | 120 |
| 100 | 160 |
经测算得乙品牌轻型汽车二氧化碳排放量的平均值为
.
（1）求表中
的值，并比较甲乙两品牌轻型汽车二氧化碳排放量的稳定性；
（2）从被检测的5辆甲品牌汽车中随机抽取2辆，求至少有1辆二氧化碳排放量超过的概率.（注:方差
，其中
为
的平均数）.
【答案】（1）
，比较见解析；（2）
.
【解析】
（1）根据
可直接计算求得，再利用方差的计算公式分别计算两者的方差，比较大小后可得乙品牌轻型汽车的二氧化碳排放量较稳定.
（2）利用列举法可得基本事件的总数和随机事件中含有的基本事件的个数，利用古典概型的概率计算公式可得所求的概率.
（1）由
，解得，
所以
，
.
.
因为
，所以乙品牌轻型汽车二氧化碳排放量较稳定.
（2）从被检测的5辆甲品牌汽车中任取2辆，所有的结果为
，
，
，
，
，
，
，
，
，
共10个.
其中至少有1辆二氧化碳排放量超过
的为：
，，，，，，共7个.
所以从被检测的5辆甲品牌汽车中任取2辆，至少有1辆氧化碳排放量超过的概率是.
练习册系列答案
轻松暑假总复习系列答案
相关题目
【题目】某茶楼有四类茶饮，假设为顾客准备泡茶工具所需的时间互相独立，且都是整数分钟，经统计以往为100位顾客准备泡茶工具所需的时间
，结果如下：
类别 | 铁观音 | 龙井 | 金骏眉 | 大红袍 |
顾客数（人） | 20 | 30 | 40 | 10 |
时间 | 2 | 3 | 4 | 6 |
注：服务员在准备泡茶工具时的间隔时间忽略不计，并将频率视为概率.
（1）求服务员恰好在第6分种开始准备第三位顾客的泡茶工具的概率；
（2）用
表示至第4分钟末已准备好了工具的顾客人数，求的分布列及数学期望.
