题目内容
【题目】某市2013年至2019年新能源汽车y(单位:百台)的数据如下表:

(Ⅰ)求y关于x的线性回归方程,并预测该市2021年新能源汽车台数;
(Ⅱ)该市某公司计划投资600台“双枪同充”(两把充电枪)、“一拖四群充”(四把充电枪)的两种型号的直流充电桩.按要求,充电枪的总把数不少于该市2021年新能源汽车预测台数,若双枪同充、一拖四群充的每把充电枪的日利润分别为25元,10元,问两种型号的充电桩各安装多少台时,才能使日利润最大,求出最大日利润.![]()
附:回归直线的斜率和截距的最小二乘法估计公式分别为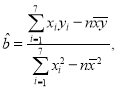
![]()
【答案】(Ⅰ)![]()
![]() ,2100台;(Ⅱ)双枪同充安装150台,一拖四群充安装450台时,每天的利润最大,最大利润为25500元.
,2100台;(Ⅱ)双枪同充安装150台,一拖四群充安装450台时,每天的利润最大,最大利润为25500元.
【解析】
(Ⅰ)计算![]() ,根据
,根据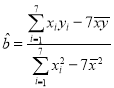 ,可得
,可得![]() ,进一步可得
,进一步可得![]() ,然后可得方程,最后代值计算,可得结果.
,然后可得方程,最后代值计算,可得结果.
(Ⅱ)假设一拖四群充,双枪同充分别安装![]() 台,
台,![]() 台,根据
台,根据![]() ,可得
,可得![]() 的范围,然后计算日利润
的范围,然后计算日利润![]() ,依据不等式可得结果.
,依据不等式可得结果.
(Ⅰ)依题意知![]() ,
,
![]() ,
,
![]() ,
,
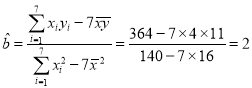 ,
,
![]() ,
,
则![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
令![]() 得:
得:![]() ,
,
故预测2021年该市新能源汽车大约有2100台.
(Ⅱ)设一拖四群充,双枪同充分别安装![]() 台,
台,![]() 台,
台,
每天的利润为![]() 元,
元,
则![]() ,即
,即![]()
![]()
![]()
所以当![]() 时,
时,![]() 取最大值25500.
取最大值25500.
故当双枪同充安装150台,一拖四群充安装450台时,
每天的利润最大,最大利润为25500元.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案
相关题目