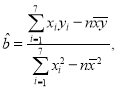题目内容
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)设![]() ,若对于任意的
,若对于任意的![]() ,
,![]() ,有
,有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析(2)![]()
【解析】
(1)求出![]() ,然后分
,然后分![]() 、
、![]() 、
、![]() 、
、![]() 四种情况讨论
四种情况讨论
(2)不妨设![]() ,则
,则![]() 可化为
可化为![]() ,构造函数
,构造函数![]() ,然后条件可转化为
,然后条件可转化为![]() 在区间
在区间![]() 上恒成立,然后利用二次函数的知识即可求出答案.
上恒成立,然后利用二次函数的知识即可求出答案.
(1)函数![]() 的定义域为
的定义域为![]() ,
,
![]() .
.
①若![]() ,则当
,则当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在区间
在区间![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在区间
在区间![]() 上单调递增.
上单调递增.
②若![]() ,则当
,则当![]() 或
或![]() 时,
时,![]() ,
,
所以函数![]() 在区间
在区间![]() ,
,![]() 上均单调递增;
上均单调递增;
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在区间
在区间![]() 上单调递减.
上单调递减.
③若![]() ,则当
,则当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在区间
在区间![]() 上单调递增.
上单调递增.
④若![]() ,则当
,则当![]() 或
或![]() 时,
时,![]() ,
,
所以函数![]() 在区间
在区间![]() ,
,![]() 上均单调递增;
上均单调递增;
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在区间
在区间![]() 上单调递减.
上单调递减.
综上所述,
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增;
上单调递增;
当![]() 时,函数
时,函数![]() 在区间
在区间![]() ,
,![]() 上均单调递增,
上均单调递增,
在区间![]() 上单调递减;
上单调递减;
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递增;
上单调递增;
当![]() 时,函数
时,函数![]() 在区间
在区间![]() ,
,![]() 上均单调递增,
上均单调递增,
在区间![]() 上单调递减.
上单调递减.
(2)不妨设![]() ,
,
则![]() 可化为
可化为![]() .
.
令![]() ,则函数
,则函数![]() 在区间
在区间![]() 上单调递增.
上单调递增.
所以![]() 在区间
在区间![]() 上恒成立.
上恒成立.
即![]() 在区间
在区间![]() 上恒成立.(*)
上恒成立.(*)
因为![]() ,所以
,所以![]() ,
,
所以,要使(*)成立,只需![]() ,
,
解得![]() .
.
故所求实数![]() 的取值范围为
的取值范围为![]() .
.

【题目】小军的微信朋友圈参与了“微信运动”,他随机选取了40位微信好友(女20人,男20人),统计其在某一天的走路步数.其中,女性好友的走路步数数据记录如下:
5860 8520 7326 6798 7325 8430 3216 7453 11754 9860
8753 6450 7290 4850 10223 9763 7988 9176 6421 5980
男性好友走路的步数情况可分为五个类别(说明:m~n表示大于等于m,小于等于n):A(0~2000步)1人,B(2001~5000步)2人,C(5001~8000步)3人,D(8001~10000步)6人,E(10001步及以上)8人.若某人一天的走路步数超过8000步被系统认定为“健康型”,否则被系统认定为“进步型”.
(1)请根据选取的样本数据完成下面的![]() 列联表,并根据此判断能否有95%以上的把握认为“认定类型”与“性别”有关?
列联表,并根据此判断能否有95%以上的把握认为“认定类型”与“性别”有关?
健康型 | 进步型 | 总计 | |
男 | 20 | ||
女 | 20 | ||
总计 | 40 |
(2)从小军的40位好友中该天走路步数不超过5000的中随机抽取3人,若![]() 表示抽到的三人分别是x,y,z,试用该表示法列举出试验所有可能的结果.若记“恰好抽到了一位女性好友”为事件A,求事件A的概率.
表示抽到的三人分别是x,y,z,试用该表示法列举出试验所有可能的结果.若记“恰好抽到了一位女性好友”为事件A,求事件A的概率.
附: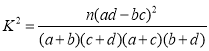 ,
,![]()
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
【题目】追求人类与生存环境的和谐发展是中国特色社会主义生态文明的价值取向.为了改善空气质量,某城市环保局随机抽取了一年内100天的空气质量指数(AQI)的检测数据,结果统计如表:
AQI |
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 重度污染 |
天数 | 6 | 14 | 18 | 27 | 25 | 10 |
(1)从空气质量指数属于[0,50],(50,100]的天数中任取3天,求这3天中空气质量至少有2天为优的概率;
(2)已知某企业每天因空气质量造成的经济损失y(单位:元)与空气质量指数x的关系式为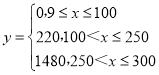 ,假设该企业所在地7月与8月每天空气质量为优、良、轻度污染、中度污染、重度污染、严重污染的概率分别为
,假设该企业所在地7月与8月每天空气质量为优、良、轻度污染、中度污染、重度污染、严重污染的概率分别为![]() .9月每天的空气质量对应的概率以表中100天的空气质量的频率代替.
.9月每天的空气质量对应的概率以表中100天的空气质量的频率代替.
(i)记该企业9月每天因空气质量造成的经济损失为X元,求X的分布列;
(ii)试问该企业7月、8月、9月这三个月因空气质量造成的经济损失总额的数学期望是否会超过2.88万元?说明你的理由.
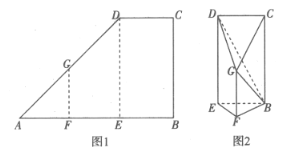
【题目】上世纪末河南出土的以鹤的尺骨(翅骨)制成的“骨笛”(图1),充分展示了我国古代高超的音律艺术及先进的数学水平,也印证了我国古代音律与历法的密切联系.图2为骨笛测量“春(秋)分”,“夏(冬)至”的示意图,图3是某骨笛的部分测量数据(骨笛的弯曲忽略不计),夏至(或冬至)日光(当日正午太阳光线)与春秋分日光(当日正午太阳光线)的夹角等于黄赤交角.

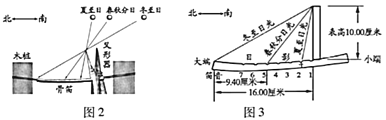
由历法理论知,黄赤交角近1万年持续减小,其正切值及对应的年代如下表:
黄赤交角 |
|
|
|
|
|
正切值 | 0.439 | 0.444 | 0.450 | 0.455 | 0.461 |
年代 | 公元元年 | 公元前2000年 | 公元前4000年 | 公元前6000年 | 公元前8000年 |
根据以上信息,通过计算黄赤交角,可估计该骨笛的大致年代是( )
A.公元前2000年到公元元年B.公元前4000年到公元前2000年
C.公元前6000年到公元前4000年D.早于公元前6000年