题目内容
【题目】在平面直角坐标系xOy中,椭圆C:![]() 的右准线方程为x=2,且两焦点与短轴的一个顶点构成等腰直角三角形.
的右准线方程为x=2,且两焦点与短轴的一个顶点构成等腰直角三角形.
(1)求椭圆C的方程;
(2)假设直线l:![]() 与椭圆C交于A,B两点.①若A为椭圆的上顶点,M为线段AB中点,连接OM并延长交椭圆C于N,并且
与椭圆C交于A,B两点.①若A为椭圆的上顶点,M为线段AB中点,连接OM并延长交椭圆C于N,并且![]() ,求OB的长;②若原点O到直线l的距离为1,并且
,求OB的长;②若原点O到直线l的距离为1,并且![]() ,当
,当![]() 时,求△OAB的面积S的范围.
时,求△OAB的面积S的范围.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() .
.
【解析】
(1)根据椭圆的几何性质可得到a2,b2;
(2)联立直线和椭圆,利用弦长公式可求得弦长AB,利用点到直线的距离公式求得原点到直线l的距离,从而可求得三角形面积,再用单调性求最值可得值域.
(1)因为两焦点与短轴的一个顶点的连线构成等腰直角三角形,所以![]() ,
,
又由右准线方程为![]() ,得到
,得到![]() ,
,
解得![]() ,所以
,所以![]()
所以,椭圆![]() 的方程为
的方程为![]()
(2)①设![]() ,而
,而![]() ,则
,则![]() ,
,
∵ ![]() , ∴
, ∴ ![]()
因为点![]() 都在椭圆上,所以
都在椭圆上,所以
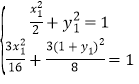 ,将下式两边同时乘以
,将下式两边同时乘以![]() 再减去上式,解得
再减去上式,解得![]() ,
,![]()
所以![]()
②由原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,得
,得![]() ,化简得:
,化简得:![]()
联立直线![]() 的方程与椭圆
的方程与椭圆![]() 的方程:
的方程: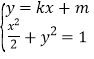 ,得
,得![]()
设![]() ,则
,则![]() ,且
,且![]()
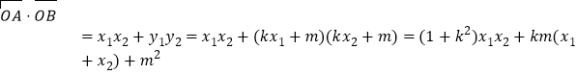
![]()
![]() ,
,
所以![]()
![]() 的面积
的面积![]()
![]() ,
,
因为![]() 在
在![]() 为单调减函数,
为单调减函数,
并且当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() 的面积
的面积![]() 的范围为
的范围为![]() .
.

练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目