题目内容
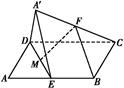
如图,在直三棱柱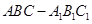 中,
中,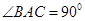 ,
,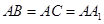 .若
.若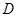 为
为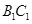 的中点,求直线
的中点,求直线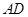 与平面
与平面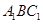 所成的角.
所成的角.
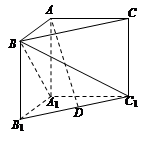
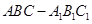 中,
中,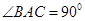 ,
,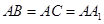 .若
.若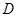 为
为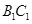 的中点,求直线
的中点,求直线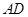 与平面
与平面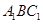 所成的角.
所成的角.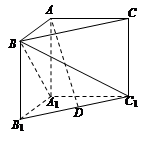
60°
试题分析:因为在直三棱柱
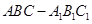 中,
中,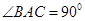 ,
,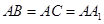 .若
.若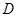 为
为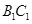 的中点,需求直线
的中点,需求直线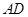 与平面
与平面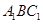 所成的角.可以建立直角坐标系,通过平面
所成的角.可以建立直角坐标系,通过平面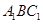 的法向量与直线
的法向量与直线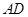 所在的向量的夹角的余弦值即为直线与平面所成角的正弦值.即可得结论.另外也可以通过构建直线所成的角,通过解三角形求得结论.
所在的向量的夹角的余弦值即为直线与平面所成角的正弦值.即可得结论.另外也可以通过构建直线所成的角,通过解三角形求得结论.试题解析:方法一:如图1以
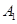 为原点,
为原点,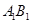 所在直线为
所在直线为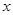 轴,
轴,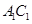 所在直线为
所在直线为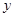 轴,
轴,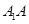 所在直线为
所在直线为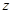 轴建系,则
轴建系,则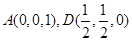 ,则
,则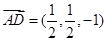 2分;
2分;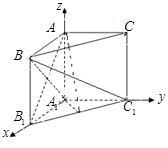
设平面A1BC1的一个法向量
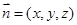 ,
,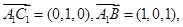 则
则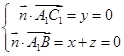 ,
,则
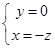 ,取
,取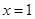 ,则
,则 6分
6分设AD与平面A1BC1所成的角为
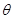 ,
,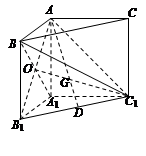
则
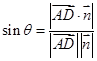 =
=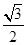 10分
10分则
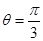 ,∴AD与平面A1BC1所成的角为
,∴AD与平面A1BC1所成的角为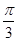 12分
12分方法二:由题意知四边形AA1B1B是正方形,故AB1⊥BA1.
由AA1⊥平面A1B1C1得AA1⊥A1C1.
又A1C1⊥A1B1,所以A1C1⊥平面AA1B1B,故A1C1⊥AB1.
从而得 AB1⊥平面A1BC1. 4分
设AB1与A1B相交于点O,则点O是线段AB1的中点.
连接AC1,由题意知△AB1C1是正三角形.
由AD,C1O是△AB1C1的中线知:AD与C1O的交点为重心G,连接OG.
知AB1⊥平面A1BC1,故OG是AD在平面A1BC1上的射影,
于是∠AGO是AD与平面A1BC1所成的角. 6分
在直角△AOG中,AG=
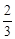 AD=
AD=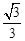 AB1=
AB1=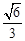 AB, AO=
AB, AO=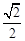 AB,
AB,所以sin∠AGO=
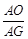 =
=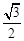 . 10分
. 10分故∠AGO=60°,即AD与平面A1BC1所成的角为60°. 12分

练习册系列答案
相关题目
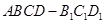 中,四边形
中,四边形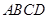 为菱形,
为菱形,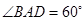 ,
,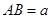 ,面
,面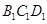 ∥面
∥面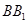 、
、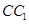 、
、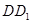 都垂直于面
都垂直于面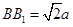 ,
,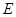 为
为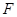 为
为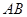 的中点.
的中点.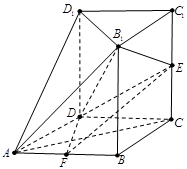
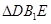 为等腰直角三角形;
为等腰直角三角形;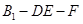 的大小.
的大小.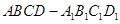 中,异面直线
中,异面直线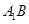 和
和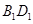 所成的角的大小为__________.
所成的角的大小为__________.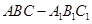 中,
中,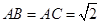 ,
,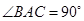 ,且异面直线
,且异面直线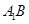 与
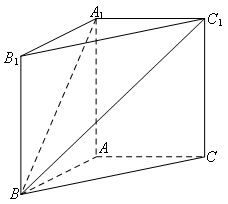
与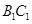 所成的角等于
所成的角等于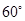 .
.
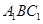 所成的角的大小.
所成的角的大小.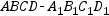 中,M是棱
中,M是棱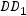 的中点,点O为底面ABCD的中心,P为棱A1B1上任一点,则异面直线OP与AM所成的角的大小为( )
的中点,点O为底面ABCD的中心,P为棱A1B1上任一点,则异面直线OP与AM所成的角的大小为( )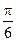
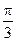
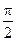
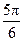
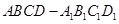 的底面是边长为1的正方形,且侧棱垂直于底面,若
的底面是边长为1的正方形,且侧棱垂直于底面,若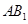 与底面
与底面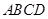 成60°角,则二面角
成60°角,则二面角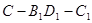 的平面角的正切值为
的平面角的正切值为