题目内容
3.设f(x)满足f(x+y)=f(x)+f(y),当x>0时f(x)<0且f(2)=-1,试问f(x)在[-6,6]上是否存在最大值.分析 利用赋值法求f(0)的值结合定义证明函数的奇偶性以及函数的单调性即可得到结论.
解答 解:令x=y=0则f(0)=2f(0),∴f(0)=0
对任意x∈R,取y=-x则f[x+(-x)]=f(x)+f(-x)=f(0)=0,
即f(-x)=-f(x),
∴f(x)是R上的奇函数,
任意取x1,x2∈R,x1<x2,则x2=x1+△x(其中△x>0),
则f(△x)<0,
∴f(x2)=f(x1+△x)=f(x1)+f(△x),
∴f(x2)-f(x1)=f(△x)<0,
即f(x2)<f(x1),
∴f(x)是R上的减函数,
即f(x)在[-6,6]上存在最大值,最大值为f(-6)=-f(6),
∵f(2)=-1,
∴f(2)+f(2)=f(2+2)=f(4),
即f(4)=-1-1=-2,
f(6)=f(4)+f(2)=-2-1=-3,
即最大值f(-6)=-f(6)=3.
点评 本题主要考查抽象函数的应用.利用赋值法,结合函数奇偶性和单调性的性质先判断函数的奇偶性和单调性是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.如图所示,在三棱台A′B′C′-ABC中,沿A′BC截去三棱锥A′-ABC,则剩余的部分是( )
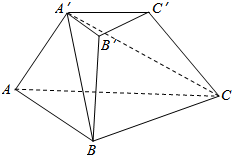

| A. | 三棱锥 | B. | 四棱锥 | C. | 三棱柱 | D. | 组合体 |