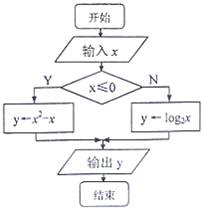
题目内容
20.A={-2,0,3},M={x|x2+(a+1)x-6=0},N={y|y2+2y-b=0}.若M∪N=A,求a,b的值.分析 由M∪N=A便得到M⊆A,N⊆A,而根据韦达定理即可知-2,3∈M,-2,0∈N,从而得到$\left\{\begin{array}{l}{-2+3=-a-1}\\{-2•0=-b}\end{array}\right.$,这样解出a,b即可.
解答 解:根据韦达定理知,方程x2+(a+1)x-6=0的两根之积为-6,方程y2+2y-b=0的两根之和为-2;
又由M∪N=A得:M⊆A,N⊆A;
∴-2,3∈M,-2,0∈N;
∴-2+3=-a-1,-2•0=-b;
∴a=-2,b=0.
点评 考查列举法、描述法表示集合,并集的概念,以及韦达定理.

练习册系列答案
相关题目
12.如图所示,在三棱台A′B′C′-ABC中,沿A′BC截去三棱锥A′-ABC,则剩余的部分是( )
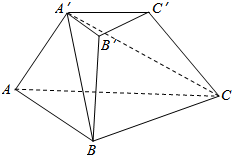

| A. | 三棱锥 | B. | 四棱锥 | C. | 三棱柱 | D. | 组合体 |
9.方程组$\left\{\begin{array}{l}{x+y=-1}\\{{x}^{2}-{y}^{2}=9}\end{array}\right.$,的解组成的集合是( )
| A. | (5,4) | B. | (5,-4) | C. | {(-5,4)} | D. | {(5,-4)} |