题目内容
3.若函数f(x)(x∈R)对任意x1≠x2,都有x1f(x1)+x2f(x2)>x1f(x2)+x2f(x1),则函数f(x)是( )| A. | 增函数 | B. | 减函数 | C. | 奇函数 | D. | 偶函数 |
分析 将不等式进行整理成(x1-x2)[f(x1)-f(x2)]>0,结合单调性的等价条件进行判断即可.
解答 解:由x1f(x1)+x2f(x2)>x1f(x2)+x2f(x1),
x1[f(x1)-f(x2)+x2[f(x2)-f(x1)]>0,
即(x1-x2)[f(x1)-f(x2)]>0,
则函数f(x)为增函数,
故选:A.
点评 本题主要考查函数单调性的判断,将条件进行整理成(x1-x2)[f(x1)-f(x2)]>0是解决本题的关键.,注意这个不等式是函数单调递增的等价形式.

练习册系列答案
相关题目
13.如图,若执行该程序,输出结果为48,则输入k值为( )


| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
18.在某项测量中,测量结果ξ服从正态分布N(0,σ2)(σ>0).若ξ在(0,1)内取值的概率为0.3,则ξ在(1,+∞)内取值的概率为( )
| A. | 0.1 | B. | 0.2 | C. | 0.3 | D. | 0.4 |
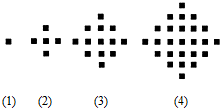 某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形. 已知MOD函数是一个求余函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(8,3)=2.如图是一个算法的程序框图,当输入的值为36时,则输出的结果为( )
已知MOD函数是一个求余函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(8,3)=2.如图是一个算法的程序框图,当输入的值为36时,则输出的结果为( )