题目内容
(理科10分)在△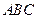 中,
中,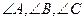 所对的边分别为
所对的边分别为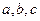 ,满足
,满足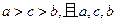 成等差数列,
成等差数列,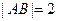 ,求点
,求点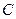 的轨迹方程.
的轨迹方程.
(文科10分)设0<a,b,c<1,求证:(1-a)b,(1-b)c,(1-c)a不同时大于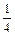 .
.
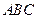 中,
中,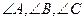 所对的边分别为
所对的边分别为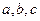 ,满足
,满足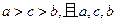 成等差数列,
成等差数列,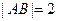 ,求点
,求点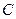 的轨迹方程.
的轨迹方程.(文科10分)设0<a,b,c<1,求证:(1-a)b,(1-b)c,(1-c)a不同时大于
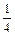 .
.(理)3x2+4y2=12
(文)证明见解析.
(文)证明见解析.
(理科)解:以AB所在直线为x轴,线段AB的中点为原点建立直角坐标系,
则点A(-1,0)B(1,0)。设C(x,y)
由题意知a+b=2c,即|CB|+|CA|=2|AB|
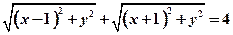
化简整理得3x2+4y2=12
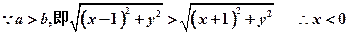
因为点C不能在x轴上,所以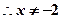
3x2+4y2="12 " (-2<x<0)是所求轨迹方程
(文科)反证法:
假设
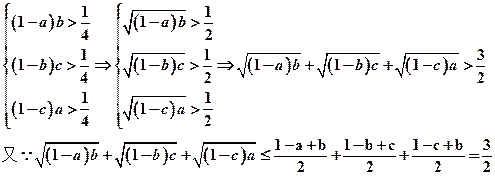
两者矛盾,所 以假设不成立。
以假设不成立。
则点A(-1,0)B(1,0)。设C(x,y)
由题意知a+b=2c,即|CB|+|CA|=2|AB|
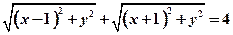
化简整理得3x2+4y2=12
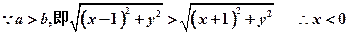
因为点C不能在x轴上,所以
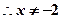
3x2+4y2="12 " (-2<x<0)是所求轨迹方程
(文科)反证法:
假设
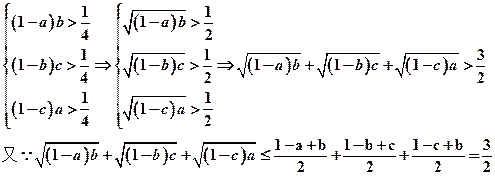
两者矛盾,所
 以假设不成立。
以假设不成立。
练习册系列答案
相关题目
 a、b、c,有下列两个条件:(1)a、b、c成等差数列;(2)a、b、c成等比数列,现给出三个结论:(1)
a、b、c,有下列两个条件:(1)a、b、c成等差数列;(2)a、b、c成等比数列,现给出三个结论:(1)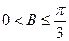 ;(2)
;(2)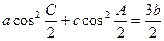 ;(3)
;(3)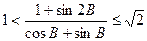 。
。 _______
_______ __________________
__________________ (II)证明:
(II)证明: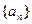 中,前
中,前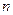 项和
项和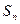 满足
满足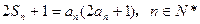 。
。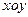 面上,设点
面上,设点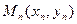 满足
满足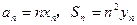 ,且点
,且点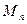 在直线
在直线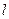 上,
上,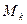 ,若称直线
,若称直线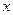 轴、直线
轴、直线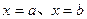 所围成的图形的面积为直线
所围成的图形的面积为直线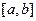 上的面积,试求直线
上的面积,试求直线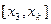 上的面积;
上的面积;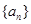 中,
中,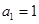 ,
,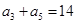 ,其前
,其前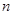 项和
项和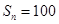 ,则
,则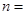 ( )
( )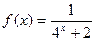 ,数列
,数列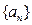 通项公式
通项公式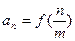
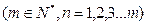
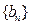 满足
满足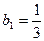 ,
,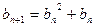 ,设
,设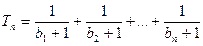
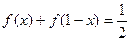 ,并求数列
,并求数列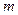 项和
项和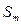
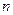 ,
,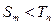 恒成立,求
恒成立,求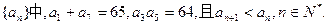
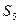
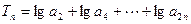 ,求Tn的最大值及此时n的值.
,求Tn的最大值及此时n的值.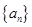 的前4项和等于4,设前n项和为
的前4项和等于4,设前n项和为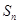 ,且
,且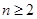 时,
时,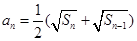 ,则
,则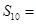 .
.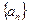 中,已知
中,已知 ,
,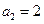 ,若对任意正整数
,若对任意正整数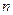 ,有
,有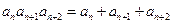 ,且
,且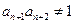 ,则该数列的前2010项和
,则该数列的前2010项和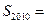
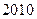 .
.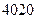 .
.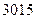 .
.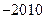 .
. 中,
中, ,
,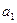 为( ).
为( ).