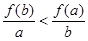题目内容
设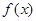 是定义在
是定义在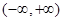 上可导函数且满足
上可导函数且满足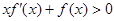 对任意的正数
对任意的正数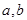 ,若
,若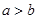 则下列不等式恒成立的是
则下列不等式恒成立的是
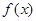 是定义在
是定义在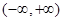 上可导函数且满足
上可导函数且满足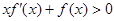 对任意的正数
对任意的正数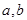 ,若
,若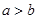 则下列不等式恒成立的是
则下列不等式恒成立的是 A.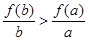 | B. | C.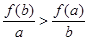 | D.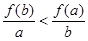 |
D
构造函数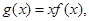 则
则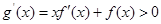 ,所以函数
,所以函数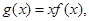 在在
在在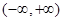 上是增函数。
上是增函数。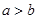 时,
时,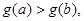 即
即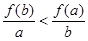
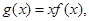 则
则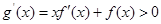 ,所以函数
,所以函数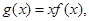 在在
在在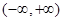 上是增函数。
上是增函数。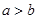 时,
时,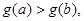 即
即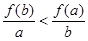

练习册系列答案
相关题目
题目内容
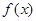 是定义在
是定义在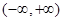 上可导函数且满足
上可导函数且满足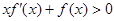 对任意的正数
对任意的正数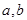 ,若
,若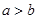 则下列不等式恒成立的是
则下列不等式恒成立的是 A.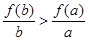 | B. | C.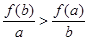 | D.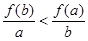 |
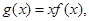 则
则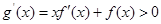 ,所以函数
,所以函数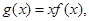 在在
在在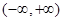 上是增函数。
上是增函数。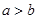 时,
时,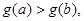 即
即