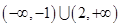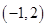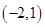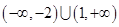题目内容
已知函数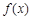 对于任意
对于任意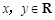 ,总有
,总有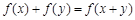 ,且x > 0时,
,且x > 0时,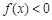 ,
,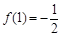 .
.
(1)求证: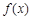 在R上是减函数;
在R上是减函数;
(2)求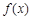 在 [– 2,2] 上的最大值和最小值.
在 [– 2,2] 上的最大值和最小值.
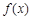 对于任意
对于任意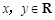 ,总有
,总有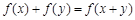 ,且x > 0时,
,且x > 0时,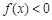 ,
,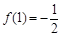 .
.(1)求证:
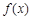 在R上是减函数;
在R上是减函数;(2)求
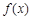 在 [– 2,2] 上的最大值和最小值.
在 [– 2,2] 上的最大值和最小值. (1) 见解析;(2) 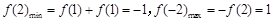
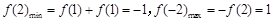
本试题主要是考查了函数的单调性和函数的最值,抽象函数具有的性质的综合运用。
(1)利用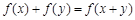 且x > 0时,
且x > 0时,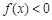 ,,结合定义得到函数单调性的证明
,,结合定义得到函数单调性的证明
(2)利用给的你该函数的单调性,和奇偶性判定给定区间的最值即可。
解:(1) 设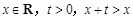
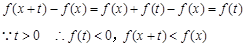
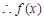 在R上是减函数
在R上是减函数
(2) 又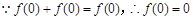 ,
,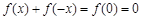
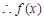 是奇函数
是奇函数
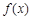 在
在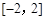 上,
上,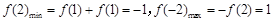
(1)利用
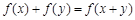 且x > 0时,
且x > 0时,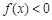 ,,结合定义得到函数单调性的证明
,,结合定义得到函数单调性的证明(2)利用给的你该函数的单调性,和奇偶性判定给定区间的最值即可。
解:(1) 设
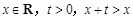
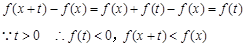
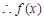 在R上是减函数
在R上是减函数(2) 又
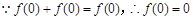 ,
,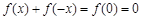
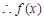 是奇函数
是奇函数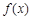 在
在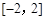 上,
上,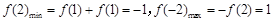

练习册系列答案
相关题目
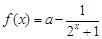 .
.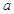 为何实数
为何实数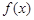 总是为增函数;(2)确定
总是为增函数;(2)确定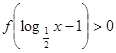
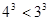
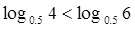
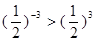
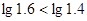
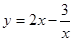 在区间
在区间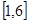 上的最小值为________,最大值为________
上的最小值为________,最大值为________ 函数
函数
 的单调区间;
的单调区间; 的取值范围.
的取值范围.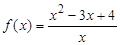 ,
,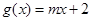 ,
,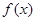 在
在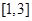 上的值域是 ;
上的值域是 ;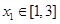 ,总存在
,总存在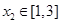 ,使得
,使得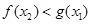 ,则实数
,则实数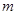 的取值范围
的取值范围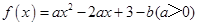 在
在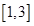 有最大值5和最小值2,求a、b的值。
有最大值5和最小值2,求a、b的值。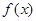 是定义在
是定义在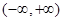 上可导函数且满足
上可导函数且满足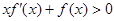 对任意的正数
对任意的正数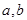 ,若
,若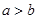 则下列不等式恒成立的是
则下列不等式恒成立的是 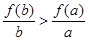

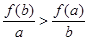
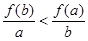
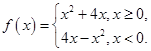 若
若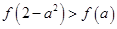 ,则实数
,则实数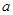 的取值范围是( )
的取值范围是( )