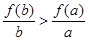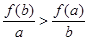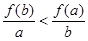题目内容
已知函数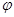 (x)=
(x)=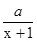 ,a是正常数。(1)若f(x)=
,a是正常数。(1)若f(x)= 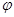 (x)+lnx,且a=
(x)+lnx,且a=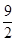 ,求函数f(x)的单调递增区间;(2)若g(x)=∣lnx∣+
,求函数f(x)的单调递增区间;(2)若g(x)=∣lnx∣+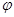 (x),且对任意的x
(x),且对任意的x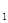 ,x
,x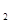 ∈(0,2〕,且x
∈(0,2〕,且x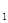 ≠x
≠x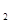 ,都有
,都有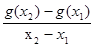 <-1,求a的取值范围
<-1,求a的取值范围
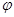 (x)=
(x)=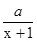 ,a是正常数。(1)若f(x)=
,a是正常数。(1)若f(x)= 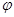 (x)+lnx,且a=
(x)+lnx,且a=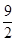 ,求函数f(x)的单调递增区间;(2)若g(x)=∣lnx∣+
,求函数f(x)的单调递增区间;(2)若g(x)=∣lnx∣+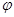 (x),且对任意的x
(x),且对任意的x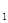 ,x
,x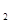 ∈(0,2〕,且x
∈(0,2〕,且x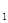 ≠x
≠x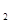 ,都有
,都有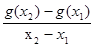 <-1,求a的取值范围
<-1,求a的取值范围(1)(0,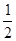 )和(2,+∞)(2)
)和(2,+∞)(2)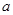 ≧
≧
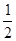 )和(2,+∞)(2)
)和(2,+∞)(2)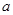 ≧
≧
本小题主要考查函数单调性的应用、利用导数研究函数的单调性、导数的几何意义、不等式的解法等基础知识,考查运算求解能力,属于基础题.
(1)先对函数y=f(x)进行求导,然后令导函数大于0(或小于0)求出x的范围,根据f′(x)>0求得的区间是单调增区间,f′(x)<0求得的区间是单调减区间,即可得到答案.
(2)设h(x)=g(x)+x,依题意得出h(x)在(0,2]上是减函数.下面对x分类讨论:①当1≤x≤2时,②当0<x<1时,利用导数研究函数的单调性从及最值,即可求得求a的取值范围.
解:⑴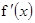 =
=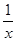 -
-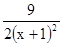 ﹥1
﹥1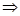
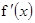 =
=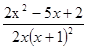 ﹥0
﹥0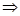 x﹥2或0﹤x﹤
x﹥2或0﹤x﹤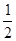 ,
,
所以函数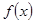 的单调增区间为(0,
的单调增区间为(0,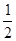 )和(2,+∞)……………………………3分
)和(2,+∞)……………………………3分
⑵因为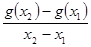 ﹤-1,所以
﹤-1,所以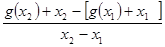 ﹤0,
﹤0,
所以F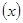 =
=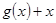 在区间(0,2】上是减函数。
在区间(0,2】上是减函数。
① 当1≦x≦2时,F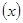 =ln
=ln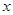 +
+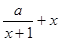
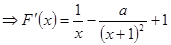 ,
,
由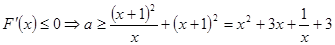 在x∈
在x∈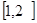 上恒成立。
上恒成立。
设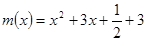 ,所以
,所以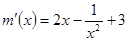 ﹥0(1≦x≦2),
﹥0(1≦x≦2),
所以 在[1,2]上为增函数,所以
在[1,2]上为增函数,所以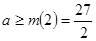
②当0﹤x﹤1时,F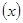 =-ln
=-ln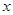 +
+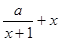
 ,
,
由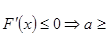 -
-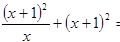 =
=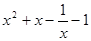 在x∈(0,1)上恒成立。
在x∈(0,1)上恒成立。
令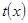 =
=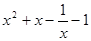
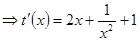 ﹥0,所以
﹥0,所以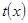 在(0,1)上为增函数,所以
在(0,1)上为增函数,所以 ,综上:
,综上: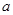 的取值范围为
的取值范围为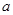 ≧
≧ …………………12分
…………………12分
(1)先对函数y=f(x)进行求导,然后令导函数大于0(或小于0)求出x的范围,根据f′(x)>0求得的区间是单调增区间,f′(x)<0求得的区间是单调减区间,即可得到答案.
(2)设h(x)=g(x)+x,依题意得出h(x)在(0,2]上是减函数.下面对x分类讨论:①当1≤x≤2时,②当0<x<1时,利用导数研究函数的单调性从及最值,即可求得求a的取值范围.
解:⑴
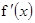 =
=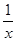 -
-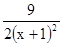 ﹥1
﹥1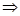
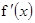 =
=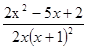 ﹥0
﹥0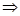 x﹥2或0﹤x﹤
x﹥2或0﹤x﹤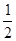 ,
,所以函数
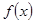 的单调增区间为(0,
的单调增区间为(0,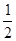 )和(2,+∞)……………………………3分
)和(2,+∞)……………………………3分⑵因为
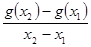 ﹤-1,所以
﹤-1,所以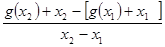 ﹤0,
﹤0,所以F
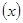 =
=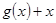 在区间(0,2】上是减函数。
在区间(0,2】上是减函数。① 当1≦x≦2时,F
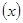 =ln
=ln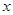 +
+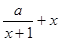
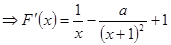 ,
,由
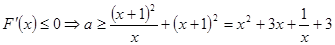 在x∈
在x∈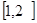 上恒成立。
上恒成立。设
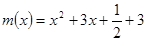 ,所以
,所以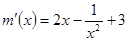 ﹥0(1≦x≦2),
﹥0(1≦x≦2),所以
 在[1,2]上为增函数,所以
在[1,2]上为增函数,所以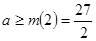
②当0﹤x﹤1时,F
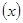 =-ln
=-ln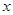 +
+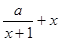
 ,
,由
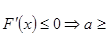 -
-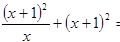 =
=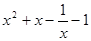 在x∈(0,1)上恒成立。
在x∈(0,1)上恒成立。令
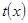 =
=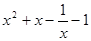
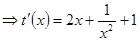 ﹥0,所以
﹥0,所以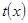 在(0,1)上为增函数,所以
在(0,1)上为增函数,所以 ,综上:
,综上: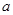 的取值范围为
的取值范围为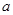 ≧
≧ …………………12分
…………………12分
练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
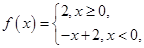 则满足不等式
则满足不等式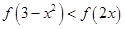 的
的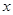 的取值范围为( )
的取值范围为( )
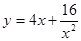
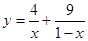 的最小值
的最小值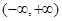 上的偶函数
上的偶函数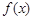 满足:
满足: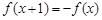 ,且在
,且在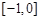 上是增函数,下面关于
上是增函数,下面关于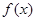 是周期函数;
是周期函数; 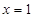 对称;
对称; 上是增函数;
上是增函数; 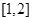 上是减函数;
上是减函数;  .
. 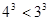
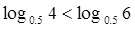
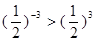
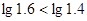
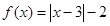 ,
,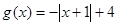 .
.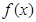 的值不大于
的值不大于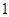 ,求
,求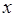 的取值范围;
的取值范围;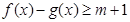 的解集为
的解集为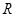 ,求
,求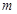 的取值范围.
的取值范围.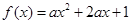 在
在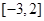 上有最大值4,则实数
上有最大值4,则实数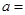 .
.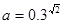 ,
,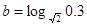 ,
,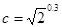 ,a,b,c从小到大排列为
,a,b,c从小到大排列为 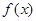 是定义在
是定义在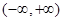 上可导函数且满足
上可导函数且满足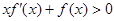 对任意的正数
对任意的正数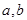 ,若
,若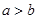 则下列不等式恒成立的是
则下列不等式恒成立的是