Question

【题目】已知三棱锥P﹣ABC的所有顶点都在球O的球面上，△ABC是边长为1的正三角形，PC为球O的直径，该三棱锥的体积为 ， 则球O的表面积为（　　）
A.4π
B.8π
C.12π
D.16π

Answer 1

【答案】A
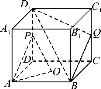
【解析】根据题意作出图形
设球心为O，球的半径r．过ABC三点的小圆的圆心为O1 ， 则OO1⊥平面ABC，
延长CO1交球于点D，则PD⊥平面ABC．
∵CO1= ，
∴OO1= ，
∴高PD=2OO1=2 ，
∵△ABC是边长为1的正三角形，
∴S△ABC= ，
∴V三棱锥P﹣ABC=××2= ，
∴r=1．则球O的表面积为4π．
故选：A．

根据题意作出图形，欲求球O的表面积，只须求球的半径r．利用截面圆的性质即可求出OO1 ， 进而求出底面ABC上的高PD，即可计算出三棱锥的体积，从而建立关于r的方程，即可求出r，从而解决问题。