Question

【题目】设B、C是定点，且均不在平面α上，动点A在平面α上，且sin∠ABC= ， 则点A的轨迹为（　　）
A.圆或椭圆
B.抛物线或双曲线
C.椭圆或双曲线
D.以上均有可能

Answer 1

【答案】D
【解析】解：以BC为轴线，B为顶点，顶角是60°（半顶角是30°），则A就是这个锥面与平面α的交线．
如果平面α只与圆锥面一面相交，如图（1），

（1）
那么A的轨迹是圆或椭圆或抛物线；
如果A与圆锥面两侧都相交（圆锥面两侧指以B为顶点向上的圆锥和向下的圆锥，就像沙漏的形状），
如图（2），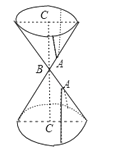

则轨迹是双曲线．
∴点A的轨迹为圆或椭圆或抛物线或双曲线．
故选：D．
以BC为轴线，B为顶点作圆锥面，使圆锥面的顶角为60°，则圆锥面上的任意一点与B连线，都能满足∠ABC=
30°，用平面α截圆锥所得的交线即为点A的轨迹．