Question

【题目】如图，在正方体ABCDA1B1C1D1中，O为底面ABCD的中心，P,Q分别为的中点．

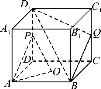
求证：(1)平面D1 BQ∥平面PAO.

(2)求异面直线QD1与AO所成角的余弦值；

Answer 1

【答案】（1）见解析； （2） .

【解析】

（1）先证明 BQ||平面PAO,再证明平面D1 BQ∥平面PAO.（2）取中点E,连接EQ,则EQ||AO,所以直线EQ和所成的锐角或直角就是异面直线QD1与AO所成的角,再解三角形求出其余弦值得解.

因为BO=DO,,

所以

因为BQ||PA,,

所以BQ||平面PAO,

因为

所以平面D1 BQ∥平面PAO.

（2）取中点E,连接EQ,则EQ||AO,

所以直线EQ和所成的锐角或直角就是异面直线QD1与AO所成的角.

设正方体的边长为2，则EQ=,

所以

所以异面直线QD1与AO所成角的余弦值为.