题目内容
7.已知tanα,tanβ是关于x的方程3x2+5x-2=0的两个实数解,且$α∈({0,\frac{π}{2}})$,$β∈({\frac{π}{2},π})$,则α+β=$\frac{3π}{4}$.分析 由韦达定理可得tanα+tanβ与tanαtanβ的值,代入两角和的正切公式可得.
解答 解:∵tanα,tanβ是方程3x2+5x-2=0的两根,
∴tanα+tanβ=-$\frac{5}{3}$,tanαtanβ=-$\frac{2}{3}$,
∴tan(α+β)=$\frac{tanα+tanβ}{1-tanαtanβ}$=-1,
$α∈({0,\frac{π}{2}})$,$β∈({\frac{π}{2},π})$,
∴α+β∈$(\frac{π}{2},\frac{3π}{2})$
∴$α+β=\frac{3π}{4}$.
故答案为:$\frac{3π}{4}$.
点评 本题考查两角和与差的三角函数公式,韦达定理的应用,角的求法,考查计算能力.

练习册系列答案
相关题目
17.某环保部门对甲、乙两类A型品牌车各抽取5辆进行CO2排放量检测,记录如下(单位:g/km).
经测算发现,乙品牌车CO2排放量的平均值为$\overline{{x}_{乙}}$=120g/km.
(Ⅰ)从被检测的5辆甲类品牌车中任取2辆,则至少有一辆CO2排放量超过130(g/km)的概率是多少?
(Ⅱ)若90<x<130,试比较甲、乙两类品牌车CO2排放量的稳定性.
| 甲 | 80 | 110 | 120 | 140 | 150 |
| 乙 | 100 | 120 | x | y | 160 |
(Ⅰ)从被检测的5辆甲类品牌车中任取2辆,则至少有一辆CO2排放量超过130(g/km)的概率是多少?
(Ⅱ)若90<x<130,试比较甲、乙两类品牌车CO2排放量的稳定性.
18.已知等差数列{an}满足a2+a4=4,a3+a5=10,则它的前10项的和S10=( )
| A. | 123 | B. | 105 | C. | 95 | D. | 23 |
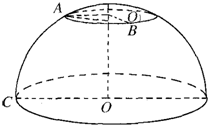 如图,在北纬60°线上,有A、B两地,它们分别在东经20°和140°线上,设地球半径为R,求A、B两地的球面距离.
如图,在北纬60°线上,有A、B两地,它们分别在东经20°和140°线上,设地球半径为R,求A、B两地的球面距离. 为了调查甲、乙两个交通站的车流量,随机选取了14天,统计每天上午8:00-12:00间各自的车流量(单位:百辆),得如下所示的统计图,
为了调查甲、乙两个交通站的车流量,随机选取了14天,统计每天上午8:00-12:00间各自的车流量(单位:百辆),得如下所示的统计图,