题目内容
(本小题满分12分)
已知数列{an}的前三项与数列{bn}的前三项对应相等,且a1+2a2+22a3+…+2n-1an=8n对任意的n∈N*都成立,数列{bn+1-bn}是等差数列.
(1)求数列{an}与{bn}的通项公式;
(2)是否存在k∈N*,使得bk-ak∈(0,1)?请说明理由.
已知数列{an}的前三项与数列{bn}的前三项对应相等,且a1+2a2+22a3+…+2n-1an=8n对任意的n∈N*都成立,数列{bn+1-bn}是等差数列.
(1)求数列{an}与{bn}的通项公式;
(2)是否存在k∈N*,使得bk-ak∈(0,1)?请说明理由.
(1)an=24-n(n∈N*),bn=n2-7n+14(n∈N*).
(2)不存在k∈N*,使得bk-ak∈(0,1).理由略
(2)不存在k∈N*,使得bk-ak∈(0,1).理由略
解:(1)已知a1+2a2+22a3+…+2n-1an=8n(n∈N*).①
n≥2时,a1+2a2+22a3+…+2n-2an-1=8(n-1)(n∈N*).②
①-②得2n-1an=8,解得an=24-n,在①中令n=1,可得a1=8=24-1,
所以an=24-n(n∈N*).(4分)
由题意b1=8,b2=4,b3=2,所以b2-b1=-4,b3-b2=-2,
∴数列{bn+1-bn}的公差为-2-(-4)=2,
∴bn+1-bn=-4+(n-1)×2=2n-6,
bn=b1+(b2-b1)+(b3-b2)+…+(bn-bn-1)
=8+(-4)+(-2)+…+(2n-8)=n2-7n+14(n∈N*).(8分)
(2)bk-ak=k2-7k+14-24-k,当k≥4时,f(k)=(k-)2+-24-k单调递增,
且f(4)=1,所以k≥4时,f(k)=k2-7k+14-24-k≥1.
又f(1)=f(2)=f(3)=0,所以,不存在k∈N*,使得bk-ak∈(0,1).(12分)
n≥2时,a1+2a2+22a3+…+2n-2an-1=8(n-1)(n∈N*).②
①-②得2n-1an=8,解得an=24-n,在①中令n=1,可得a1=8=24-1,
所以an=24-n(n∈N*).(4分)
由题意b1=8,b2=4,b3=2,所以b2-b1=-4,b3-b2=-2,
∴数列{bn+1-bn}的公差为-2-(-4)=2,
∴bn+1-bn=-4+(n-1)×2=2n-6,
bn=b1+(b2-b1)+(b3-b2)+…+(bn-bn-1)
=8+(-4)+(-2)+…+(2n-8)=n2-7n+14(n∈N*).(8分)
(2)bk-ak=k2-7k+14-24-k,当k≥4时,f(k)=(k-)2+-24-k单调递增,
且f(4)=1,所以k≥4时,f(k)=k2-7k+14-24-k≥1.
又f(1)=f(2)=f(3)=0,所以,不存在k∈N*,使得bk-ak∈(0,1).(12分)

练习册系列答案
相关题目
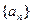 ,定义其倒均数是
,定义其倒均数是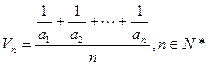 。
。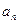 }的倒均数是
}的倒均数是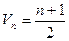 ,求数列{
,求数列{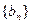 的首项为-1,公比为
的首项为-1,公比为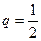 ,其倒数均为
,其倒数均为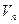 ,若存在正整数k,使
,若存在正整数k,使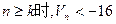 恒成立,试求k的最小值。
恒成立,试求k的最小值。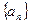 满足
满足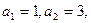 且
且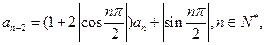
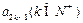 ;
;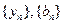 满足
满足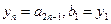 ,且
,且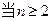 时
时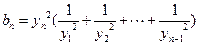 .证明当
.证明当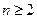 时,
时, 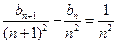 ;
;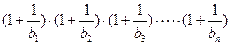 与4的大小关系.
与4的大小关系.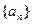 的公差为2 , 若
的公差为2 , 若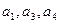 成等比数列, 则
成等比数列, 则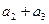 的值为( )
的值为( )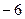

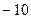
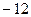
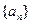 中,
中,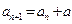 (
(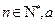 为常数),若平面上三个不重合的点
为常数),若平面上三个不重合的点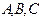 共线L,
共线L,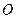 是直线L外一点,且
是直线L外一点,且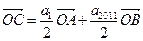 ,则
,则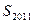 等于 ( )
等于 ( )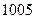

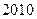
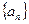 是等差数列,则数列
是等差数列,则数列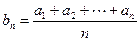 (
(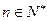 )也为等
)也为等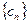 是等比数列,且
是等比数列,且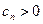 ,则有
,则有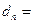 也是等比数列.
也是等比数列.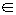 Z}中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,…将数列{an}各项按从小到大的原则写成如下的三角形数表.
Z}中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,…将数列{an}各项按从小到大的原则写成如下的三角形数表. 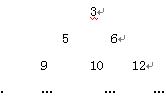 则a95=________
则a95=________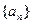 和等比数列
和等比数列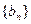 ,
,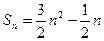 ,
,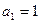 ,
,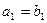 ,
,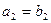 ;
;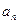 和等比数列
和等比数列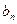 ;
;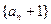 的前n项和
的前n项和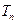 与等比数列
与等比数列 。
。